Апериодическая разрядка конденсатора

Апериодической разрядкой конденсатора, заряженного до напряжения , через резистор и катушку индуктивности называется разрядка, при которой напряжение на конденсаторе монотонно спадает от значения до нуля, т. е. не происходит перезарядки конденсатора. С энергетической точки зрения это означает, что при разрядке конденсатора отдаваемая им энергия лишь в малой доле переходит в энергию магнитного поля катушки, а большая ее часть поглощается в резисторе. Начиная с некоторого момента времени, в тепло переходит не только оставшаяся энергия электрического поля конденсатора, но и энергия, которая запаслась в магнитном поле катушки.

Апериодическое решение однородного дифференциального уравнения, т. е. в рассматриваемом случае апериодический характер свободного процесса (разрядки конденсатора), имеет место, если корни характеристического уравнения ( 14.35) действительные, т. е. если

или

Назовем критическим сопротивлением контура такое его наименьшее значение, при котором свободный процесс имеет еще апериодический характер:

Корни действительные и различные, если выполняется неравенство .

Общее решение однородного дифференциального уравнения второго порядка, и в частности ( 14.32), при различных корнях записывается в виде

где при условии (14.36) - действительные постоянные интегрирования, определяемые из начальных условий, а - действительные и различные корни характеристического уравнения.

Заметим, что корни обязательно отрицательные, так как свободный процесс должен быть затухающим во времени.

Согласно ( 14.31) ток

При разрядке конденсатора установившееся напряжение на нем и ток равны нулю, поэтому их переходные значения равны свободным:

Из начальных условий определим значения постоянных интегрирований. Подставив начальные условия в (14.38) и (14.39), получим

откуда

Приу этих значениях постоянных интегрирования напряжение (14.38) и ток (14.39)

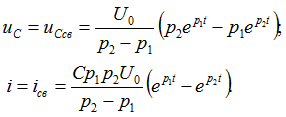
Так как произведение корней характеристического уравнения равно его свободному члену, т. е. , то

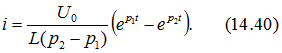
Напряжение на индуктивности

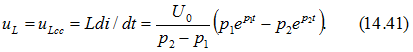
Ток и напряжения на емкостном и на индуктивном элементах состоят из двух экспоненциальных составляющих, коэффициенты затухания которых равны и определены равенствами ( 14.35).

Рис. 14.17

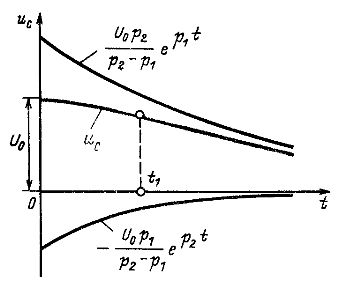
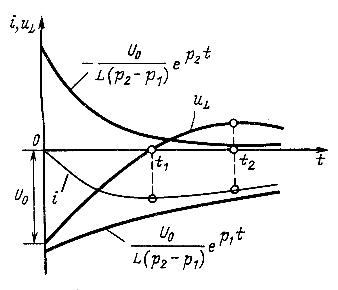
Кривые изменения и их составляющих приведены на рис. 14.17 и 14.18. Они показывают, что напряжение монотонно уменьшается с начального значения , а ток, возрастая от нуля, достигает максимума, а затем также уменьшается. Касательная к кривой в начале координат горизонтальна, так как производная напряжения пропорциональна току и в начальный момент равна нулю.

Поскольку , максимум кривой тока и точка перегиба кривой напряжения получаются в один и тот же момент времени . Это время можно найти, приравняв нулю производную .

Напряжение на индуктивном элементе изменяется от значения , так как при t = 0 и ток, и напряжение равны нулю, и, следовательно, напряжения и равны по абсолютному значению. Напряжение по абсолютному значению сначала уменьшается, затем проходит через нуль в момент, когда ток максимален (что следует из соотношения ), и возрастает до некоторого положительного максимума, после чего уменьшается и стремится к нулю. Пока ток алгебраически уменьшается (в интервале от нуля до ), ЭДС самоиндукции поддерживая его, будет согласно закону Ленца положительной, а напряжение - отрицательным. Когда ток начинает алгебраически возрастать, ЭДС самоиндукции противодействует ему и будет отрицательной, а напряжение - положительным.

Максимум кривой и точка перегиба кривой i получаются в один и тот же момент времени , что следует в свою очередь из равенства . Этот момент времени можно найти, приравняв нулю производную .

Отметим также влияние индуктивности на протекание процесса. Из выражений (14.35) следует, что увеличение индуктивности L приводит к уменьшению абсолютных значений и, стало быть, к замедлению нарастания тока и спада напряжения н конденсаторе. Наоборот, при малой индуктивности L ток растет быстро и быстро спадает напряжение на конденсаторе. Такой случай фактически получается при разрядке конденсатора через резистор (см. раздел).

Рис. 14.18

Дополнительно по теме