Столкновения электронов с атомами или молекулами газа

Движение молекул, а также заряженных частиц (электронов и ионов) в газовой среде зависит от концентрации газа n (числа молекул в 1 м³ газа).

Она связана с давлением р и температурой газа Т соотношением

При количественном учете актов столкновений атомов (молекул) газа обычно пользуются средней длиной свободного пробега молекул или обратной ей величиной эффективного сечения газа Qм (среднего числа столкновений на 1 м пути):

Здесь q - газокинетическое сечение молекулы (атома), м²; - средняя длина свободного пробега молекул при p=1Па и Т=273К; р0 = р273/Т- давление газа, приведенное к 273 К.

Соответственно

где Qm0 - эффективное сечение газа при р=1 Па и Т = 273К.

Значения для некоторых газов даны в табл. 3-10.

Газ	He	Ne	Ar	H2	N2	O2	Пары Na	Пары Hg

При движении электронов в газе средняя длина их свободного пробега оказывается согласно кинетической теории газа в раз больше (вследствие малых размеров и относительно большей скорости электрона):

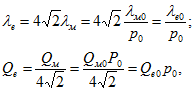
где Qe - эффективное сечение газа для электронов; Qe0--эффективное сечение газа для электронов при р=1 Па и Т = 273 К.

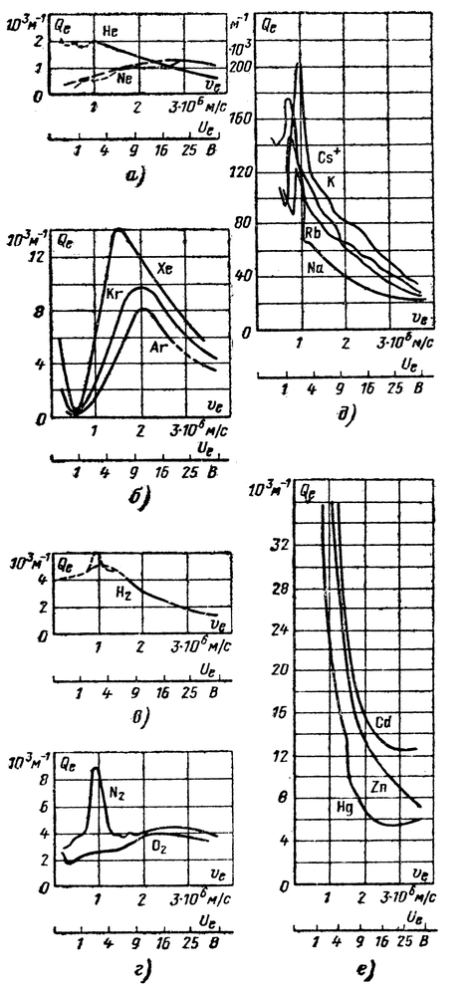
Однако газокинетическая длина свободного пробега электрона дает лишь приближенное представление о движении электронов в газе. Действительное значение оказывается зависящим также от скорости движения (энергии) электронов. Эти зависимости для некоторых газов и паров металлов приведены на рис. 3-16, а-д.

Рис. 3.16

Скорость электрона Ve связана с проходимой разностью потенциалов Ue соотношением

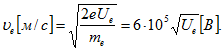
Столкновения электронов с нейтральными невозбужденными атомами могут быть упругими или неупругими I рода. При упругих столкновениях не происходит перехода кинетической энергии электрона во внутреннюю энергию атома.

Кинетическая энергия, теряемая электроном и приобретаемая атомом, невелика из-за большой разности масс электрона и атома Ма (доля теряемой в среднем энергии порядка ).

При неупругих столкновениях I рода часть кинетической энергии электрона сообщается атому в виде энергии возбуждения или ионизации атома.

Полное эффективное сечение газа для столкновений с электронами Qe складывается из эффективных сечений упругих Qеy, возбуждающих Qев и ионизирующих Qei соударений:

Вероятности упругого удара, возбуждения и ионизации представляют собой отношения эффективных сечений для соответствующих столкновений к полному эффективному сечению:

соответственно этому

Эффективные сечения для упругих и неупругих столкновений зависят от рода газа, его давления и энергии электрона. Вероятности столкновений соответствующих видов оказываются зависящими от энергии электрона и рода газа.

Рис. 3-17. Зависимость вероятности ионизации соответствующих атомов от энергии электронов.

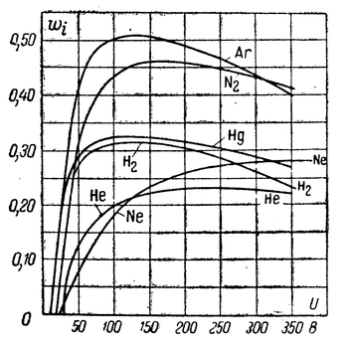
На рис. 3-17 приведена зависимость вероятности ионизации некоторых атомов от энергии электрона, выраженной в вольтах. Минимальная энергия, необходимая для ионизации или возбуждения данного атома, характеризуется соответственно потенциалами ионизации Ui или возбуждения Uв.

В табл. 3-11 приведены потенциалы возбуждения резонансных уровней Uрез, метастабильных состояний Uмет, потенциалы однократной ионизации Ui и двукратной ионизации ; некоторых газов и паров.

Таблица 3-11.

Значения некоторых газов и паров
Вещество
Н2	11,1	-	15,4	-
Не	20,86-21,2	19,72-20,51	24,47	75
Ne	16,62-16,79	16,57-16,66	21,47	63
Аг	11,56-11,77	11,49-11,66	15,69	44
Кг	9,98-10,59	9,86-10,51	13,94	-
Хе	8,39-9,52	8,28-9,40	12,08	-
Li	1,84	-	5,37	-
Na	2,1	-	5,12	-
К	1,60-1,61	-	4,32	-
Rb	1,55-1,58	-	4,14	-
Cs	1,38-1,45	-	3,87	-
Mg	2,70-4,33	2,7	7,61	-
Ва	1,56-2,23	1,11-1,41	5,19	-
Zn	4,01-5,77	3,99-4,01	9,36	-
Cd	3,78-5,39	3,71-3,93	8,96	-
Hg	4,86-6,67	4,66-5,43	10,38	30

В тех газах или парах, атомы которых обладают большим сродством к электрону, ёозможно прилипание электронов к атомам с образованием отрицательных ионов. К таким газам относятся, например, О2, F2, Cl2, NО2, пары воды, пары Li, Na, К, Rb, Cs и др.

Количественно эффект прилипания характеризуется вероятностью прилипания h тем большей, чем больше энергия сродства, или коэффициентом прилипания , дающим число прилипаний электрона на 1 м пути:

где ke - коэффициент подвижности электронов; Е - напряженность электрического поля в разрядном пространстве; е и mе - заряд и масса электрона.

Зависимость полного эффективного сечения атомов и молекул некоторых газов и паров для электрона от скорости или энергии Uе налетающего электрона при 133 Па.

Эффект прилипания проявляется слабо при значительных напряженностях электрического поля, имеющих место обычно при зажигании, а иногда и горении разряда. При гашении разряда, когда с разрядного промежутка снимается напряжение, прилипание идет интенсивно и существенно влияет на процесс спада концентрации электронов.

Процесс образования нейтрального атома (молекулы) при воссоединении электрона и положительного иона называется электронно-ионной рекомбинацией. Электронно-ионная рекомбинация может протекать двояким путем:

1. Рекомбинация в двойном ударе (радиационная) - непосредственное взаимодействие электрона и иона ,в газовой среде, при котором избыточная энергия вы-деляется в виде светового кванта. Его энергия , где телекинетическая энергия электрона до рекомбинации.

Изменение концентрации электронов и ионов в результате рекомбинации этого вида описывается уравнением

где nе и ni - концентрации электронов и ионов; - коэффициент рекомбинации; м3/с.

Для рекомбинации частиц нужно, чтобы скорость их относительного движения была не слишком велика. Поэтому коэффициент рекомбинации зависит от температуры электронного газа Те (в равновесной плазме - от температуры газа Т).

Таблица 3-12

Коэффициенты радиационной рекомбинации
Род ионов
H2		-
Ar		3100
Cs		2000
Hg		2000

В табл. 3-12 приведены значения коэффициента радиационной рекомбинации для водорода, аргона, паров цезия и ртути. Концентрации электронов nе и ионов ni обычно тем выше, чем больше давление газа в разряде. В связи с этим рекомбинация в двойном ударе имеет место в разряде сравнительно высокого давления при достаточно большом разрядном токе.

В молекулярных газах возможна рекомбинация молекулярного иона с электроном, при которой выделяющаяся энергия идет на диссоциацию молекулы на атомы (диссоциативная рекомбинация). Коэффициент диссоциативной рекомбинации порядка , т. е. интенсивность этого процесса велика даже при сравнительно низких давлениях.

2. Рекомбинация в тройном соударении. В этм случае ион сталкивается с электроном в присутствии третьей частицы, которой и передается избыточная энергия. Такой частицей обычно является атом газа, а поэтому интенсивность процесса пропорциональна не только но и концентрации нейтральных атомов газа. Вследствие этого рекомбинация в тройном соударении существенна при весьма высоких давлениях газа.

Частным случаем рекомбинации в тройном соударении является рекомбинация на стенках и электродах. Резко ограниченные возможности перемещения электронов и ионов на этих поверхностях делают вероятность рекомбинации близкой к единице, и исчезновение электронов и ионов определяется исключительно условиями их ухода из разряда на эти поверхности. При низких давлениях газа, когда эти условия облегчены, рекомбинация на стенках является основной.

В электроотрицательных газах, где образуются наряду с положительными и отрицательные ионы, возникает ион-ионная рекомбинация. Коэффициенты ион-ионной рекомбинации на 3-4 порядка больше . Поэтому интенсивность ион-ионной рекомбинации определяется главным образом интенсивностью генерации отрицательных ионов, т. е. коэффициентом аа.

Разновидностью неупругого удара II рода (наряду с процессами рекомбинации) является взаимодействие возбужденного атома с электроном или нейтральным атомом, которым передается энергия возбуждения. При этом происходит безызлучательный переход возбужденного атома в нормальное состояние. Вероятность такого процесса велика для метастабильных атомов, имеющих большое время жизни.

Другим результатом столкновения возбужденного (метастабильного) атома с быстрым электроном или световым квантом является переход электрона атома на более высокий уровень возбуждения (ступенчатое возбуждение) или полный отрыв электрона от атома (ступенчатая ионизация).

Эти процессы существенны при достаточных концентрациях возбужденных атомов и электронов, т. е. при достаточно больших (тысячи Паскалей) давлениях и больших токах разряда.

Дополнительно по теме