Расчет несимметричных режимов трехфазных цепей со статической нагрузкой

При расчете симметричных режимов трехфазных цепей двигатели можно заменять эквивалентными схемами, состоящими из трех одинаковых сопротивлений, соединенных звездой или треугольником. Падения напряжения в фазах генератора, если это необходимо, могут учитываться как напряжения на трех одинаковых сопротивлениях.

Такие простые эквивалентные схемы для двигателей и такой простой учет падений напряжения в генераторах оказываются непригодными для расчета несимметричных режимов. Анализ процессов в трехфазных электрических машинах (двигателях и генераторах) при несимметричных режимах показывает, что для них справедливы более сложные эквивалентные схемы, не удовлетворяющие принципу взаимности. В настоящее время для расчета несимметричных режимов в трехфазных цепях с трехфазными двигателями почти исключительно пользуются специальным методом расчета - методом симметричных составляющих.

В этом параграфе ограничимся исследованием несимметричных режимов цепей при следующих двух условиях:

имеется только статическая нагрузка (нет электродвигателей);
падения напряжения в фазах генератора не учитываются.

При двух указанных ограничениях расчеты несимметричных режимов трехфазных цепей не содержат ничего принципиально нового и могут выполняться любыми методами, известными из предыдущих глав. Последующее содержание иллюстрирует это положение на ряде частных примеров.

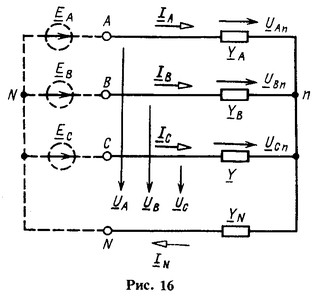
Пусть заданы несимметричные фазные напряжения на выводах несимметричного приемника (рис. 16). Определим токи. Заданные напряжения можно всегда приписать источникам ЭДС (показаны штриховой линией)

В схеме два узла, поэтому целесообразно применить для расчета метод узловых потенциалов.

Обозначив напряжение между нейтральными точками приемника и источника питания через , найдем смещение нейтрали

где - проводимости ветвей, и токи

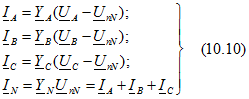
В предельном случае при , и, следовательно, напряжения на фазах приемника равны фазным напряжениям источника питания. При этом условии ток в каждой фазе может быть вычислен по закону Ома независимо от токов остальных фаз.

При отсутствии нейтрального провода расчет можно вести в таком же порядке. Изменится лишь выражение для напряжения поскольку , а именно

Однако обычно при отсутствии нейтрального провода бывают заданы не фазные, а линейные напряжения на выводах цепи. Сумма линейных напряжений равна нулю как сумма напряжений вдоль замкнутого контура, соединяющего выводы А, В и С:

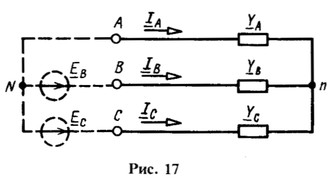
Учитывая эту связь, достаточно задать два линейных напряжения. Можно, например, их задать двумя источниками напряжения (рис. 17) с ЭДС Так как в схеме рис. 17 потенциалы точек N и А одинаковы, то

Рассмотрим простейшую схему с несимметричным приемником, соединенным треугольником (рис. 18). Если известны линейные напряжения между выводами А', В', С', к которым присоединены фазы приемника, то задача определения токов элементарно проста. Ток в каждой ветви треугольника определяется по закону Ома, а затем находятся токи в проводах питающей линии.

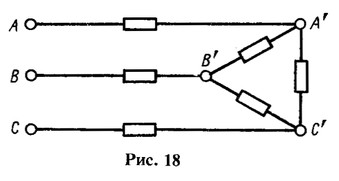
Однако обычно бывают известны напряжения не на выводах приемника, а на выводах А, В, С источника питания, поэтому расчет несколько усложняется. Проще всего его провести, заменив треугольник сопротивлений эквивалентной звездой. В результате получается схема на рис. 17, и токи в ней рассчитываются, как указано выше. По найденным токам определяются напряжения на выводах треугольника в исходной схеме (рис. 18) и затем токи в ветвях треугольника.

К преобразованию схемы следует прибегать и в случае цепи с несколькими приемниками, имеющими различные схемы соединений. Так, например, при расчете токов в цепи, представленной на рис. 19, звезду 2 следует преобразовать в эквивалентный треугольник, ветви которого будут параллельны ветвям треугольника 3. После замены каждой пары параллельных ветвей треугольников одной ветвью получается рассмотренная выше схема (рис. 18).

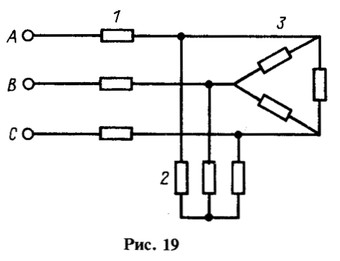
Заметим, что преобразование треугольника 3 в звезду не дало бы возможности продолжить упрощение схемы. Потенциалы нейтральных точек получившейся звезды и звезды 2 в общем случае различны, и нейтральные точки этих звезд нельзя соединять друг с другом.

Если элементы цепи индуктивно связаны друг с другом, то расчет может быть выполнен, например, путем решения уравнений Кирхгофа, составленных для токов в ветвях или же для контурных токов. В ряде случаев целесообразно исключить индуктивные связи, перейдя к эквивалентным схемам.

Дополнительно по теме