Резонанс напряжений и токов в сложных контурах
Резонанс напряжений и токов в сложных контурах
Резонанс напряжений и токов в сложных контурах
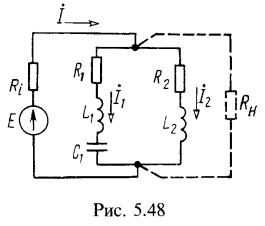
1. Параметры параллельного контура (рис. 5.48) имеют следующие значения:![]()
Найти частоты резонанса токов, напряжений и сопротивления цепи при этих частотах. Чему равна добротность контура и эквивалентная добротность при его подключении к источнику с внутренним сопротивлением ![]() ? Какова при этом полоса пропускания контура? Определить область частот, при которых модуль сопротивления параллельного контура больше 10 кОм. Определить эквивалентные резистивные и реактивные сопротивления контура на границах этой области. При каком условии сопротивление контура при резонансе токов будет иметь максимально возможное значение?
? Какова при этом полоса пропускания контура? Определить область частот, при которых модуль сопротивления параллельного контура больше 10 кОм. Определить эквивалентные резистивные и реактивные сопротивления контура на границах этой области. При каком условии сопротивление контура при резонансе токов будет иметь максимально возможное значение?
Как нужно подключить контур к источнику синусоидальной ЭДС с амплитудой ![]() и внутренним сопротивлением
и внутренним сопротивлением ![]() , чтобы мощность, выделенная в контуре, была максимальна и чему она равна?
, чтобы мощность, выделенная в контуре, была максимальна и чему она равна?
Решение:
Частота резонанса токов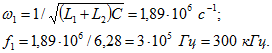 Сопротивление контура при этой частоте
Сопротивление контура при этой частоте![]() Частота резонанса напряжений:
Частота резонанса напряжений:![]()
При этой частоте сопротивления каждой из ветвей и всего параллельного контура соответственно равны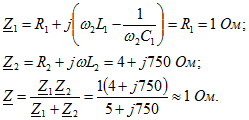 Добротность контура
Добротность контура![]() и эквивалентная добротность
и эквивалентная добротность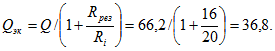 Полосу пропускания найдем по формуле
Полосу пропускания найдем по формуле![]() Для определения области частот, при которых модуль сопротивления параллельного контура больше 10 кОм, используем формулу для модуля полного сопротивления:
Для определения области частот, при которых модуль сопротивления параллельного контура больше 10 кОм, используем формулу для модуля полного сопротивления:![]() Отсюда найдем обобщенную расстройку
Отсюда найдем обобщенную расстройку ![]() и с учетом
и с учетом ![]() соответствующую ей абсолютную расстройку:
соответствующую ей абсолютную расстройку: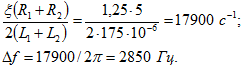 Искомая область частот, при которой
Искомая область частот, при которой ![]() , определяют из неравенства
, определяют из неравенства ![]()
Эквивалентные резистивное и реактивное сопротивления при ![]()
![]() Вычислим максимально возможное сопротивление параллельного контура при резонансе токов. Оно имеет место тогда, когда вся индуктивность сосредоточена в одной из ветвей, а емкость — в другой. В этом случае
Вычислим максимально возможное сопротивление параллельного контура при резонансе токов. Оно имеет место тогда, когда вся индуктивность сосредоточена в одной из ветвей, а емкость — в другой. В этом случае![]() Наконец, решим вопрос об условиях подключения контура к источнику ЭДС, с тем, чтобы в нем была выделена максимальная мощность. Как известно, это будет в случае, если сопротивление контура при резонансе
Наконец, решим вопрос об условиях подключения контура к источнику ЭДС, с тем, чтобы в нем была выделена максимальная мощность. Как известно, это будет в случае, если сопротивление контура при резонансе ![]() равно сопротивлению источника
равно сопротивлению источника ![]() Для этого используем свойство сложного параллельного контура изменять свое резонансное сопротивление при перераспределении его реактивных элементов по отдельным ветвям без изменения частоты резонанса токов. Обозначим значение индуктивности правой ветви контура, удовлетворяющей требованиям задачи
Для этого используем свойство сложного параллельного контура изменять свое резонансное сопротивление при перераспределении его реактивных элементов по отдельным ветвям без изменения частоты резонанса токов. Обозначим значение индуктивности правой ветви контура, удовлетворяющей требованиям задачи ![]() , через
, через ![]() , тогда получим
, тогда получим![]() Отсюда
Отсюда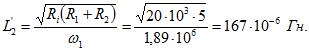 Максимальная мощность, выделяемая в контуре при указанном условии,
Максимальная мощность, выделяемая в контуре при указанном условии,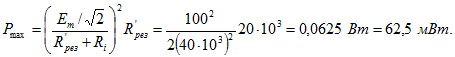 2. Как надо перераспределить индуктивности катушек
2. Как надо перераспределить индуктивности катушек ![]() между отдельными ветвями контура задачи 1., чтобы при той же частоте резонанса токов полное сопротивление параллельного контура равнялось 12 кОм?Решение:
между отдельными ветвями контура задачи 1., чтобы при той же частоте резонанса токов полное сопротивление параллельного контура равнялось 12 кОм?Решение:
Пусть при требуемых условиях (![]() остается той же) полная индуктивность контура
остается той же) полная индуктивность контура ![]() распределится гак, чтобы в левой ветви была индуктивность
распределится гак, чтобы в левой ветви была индуктивность ![]() , а в правой
, а в правой ![]() . При этом полное сопротивление контура при частоте резонанса токов:
. При этом полное сопротивление контура при частоте резонанса токов: ![]()
Отсюда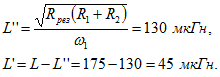 3. Определить значение сопротивления
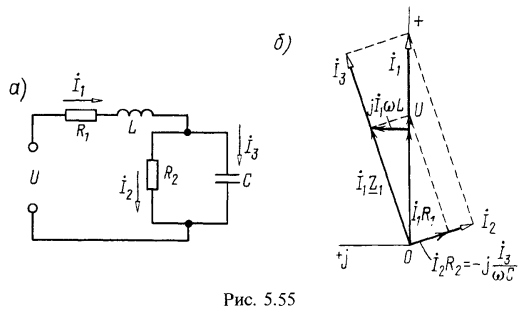
3. Определить значение сопротивления ![]() , при котором в цепи рис. 5.55, а имеется резонанс напряжений на частоте
, при котором в цепи рис. 5.55, а имеется резонанс напряжений на частоте ![]() . Вычислить токи. Построить векторную диаграмму. Дано:
. Вычислить токи. Построить векторную диаграмму. Дано: ![]() .
.
Решение:
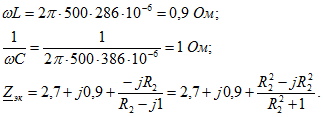
При резонансе реактивная составляющая сопротивления ![]() должна быть равна нулю, т.е.
должна быть равна нулю, т.е. ![]() , откуда
, откуда ![]()
При найденном значении ![]() полное сопротивление цепи имеет только вещественную составляющую:
полное сопротивление цепи имеет только вещественную составляющую:
![]()
Токи в неразвствленной части цепи и параллельных ветвях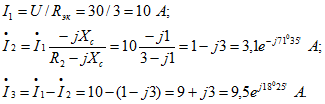 На рис. 5.55,б начерчена векторная диаграмма. На основе расчета отложены векторы токов
На рис. 5.55,б начерчена векторная диаграмма. На основе расчета отложены векторы токов ![]() , далее построены векторы
, далее построены векторы![]() Наконец, построен вектор, являющийся суммой векторов напряжений на неразветвленном
Наконец, построен вектор, являющийся суммой векторов напряжений на неразветвленном ![]() и на параллельном
и на параллельном ![]() участках.
участках.
Смотри полное содержание по представленным решенным задачам.

