Импульсные характеристики. Расчет переходных процессов при импульсных воздействиях
Импульсные характеристики. Расчет переходных процессов при импульсных воздействиях
Импульсные характеристики. Расчет переходных процессов при импульсных воздействиях
1. Рассчитать импульсные характеристики цепи (см. рис. 8.38) при воздействии на вход цепи источника ЭДС, полагая, что реакцией является: а) ток в перазветвлениой части цепи; б) напряжение на резистивном элементе.Решение:
Переходные характеристики цепи определены в задаче 1 предыдущего раздела: ![]()
![]() . Для определения импульсных характеристик цепи используем формулу:
. Для определения импульсных характеристик цепи используем формулу: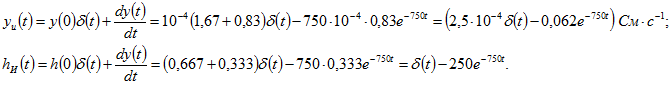 2. Цепь, состоящая из последовательно соединенных R=50 Ом и L=2,5 Гн, включается под действие напряжения
2. Цепь, состоящая из последовательно соединенных R=50 Ом и L=2,5 Гн, включается под действие напряжения ![]() . Найти ток в цепи и построить его кривую.Решение:
. Найти ток в цепи и построить его кривую.Решение:
Составляем дифференциальное уравнение по второму закону Кирхгофа:![]() Решение его
Решение его![]() где
где ![]() — общий интеграл уравнения (8.1) без правой части,
— общий интеграл уравнения (8.1) без правой части, ![]() — частное решение уравнения (8.1).
— частное решение уравнения (8.1).
Найдем ![]() . Как известно из курса математики, частное решение рассматриваемого линейного дифференциального уравнения определяется в форме показательной функции:
. Как известно из курса математики, частное решение рассматриваемого линейного дифференциального уравнения определяется в форме показательной функции:![]() Подставляя это значение в (8.1), получим
Подставляя это значение в (8.1), получим ![]() , откуда
, откуда ![]() . Подставляя значение В в (8.3), получим
. Подставляя значение В в (8.3), получим
![]() Переходный ток i [см. формулу (8.2)]
Переходный ток i [см. формулу (8.2)]![]() Для определения постоянной интегрирования А используем начальное условие
Для определения постоянной интегрирования А используем начальное условие ![]() :
: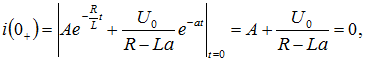 отсюда
отсюда![]() Таким образом,
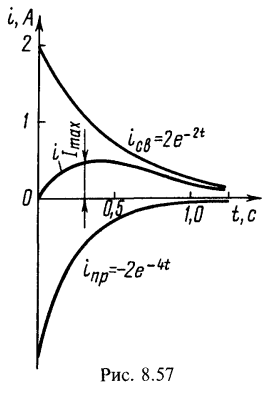
Таким образом,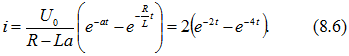 Кривая тока изображена на рис. 8.57.
Кривая тока изображена на рис. 8.57.
Ток имеет максимум, найдем его![]() Приравнивая эту производную нулю, получим момент времени
Приравнивая эту производную нулю, получим момент времени ![]() , при котором значение тока максимально
, при котором значение тока максимально![]() отсюда
отсюда ![]()
Подставив это значение в формулу (8.6), найдем![]()
3. Цепь, состоящая из последовательно соединенных R и L, включается на прямоугольный импульс напряжения U, действующий в течение времени ![]() (рис. 8.58, а). Найти выражение тока i и напряжение на индуктивной катушке
(рис. 8.58, а). Найти выражение тока i и напряжение на индуктивной катушке ![]() в зависимости от времени. Построить кривые
в зависимости от времени. Построить кривые ![]() .Решение:
.Решение:
а. Классический способ. Для интервала времени от t=0 до ![]() ток определяется так же, как и при включении той же цепи на постоянное напряжение U:
ток определяется так же, как и при включении той же цепи на постоянное напряжение U: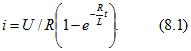
Напряжение на индуктивной катушке![]() При
При ![]() воздействие на цепь отсутствует, поэтому ток содержит только свободную составляющую. Она определяется энергией, накопленной в магнитном поле за время от 0 до
воздействие на цепь отсутствует, поэтому ток содержит только свободную составляющую. Она определяется энергией, накопленной в магнитном поле за время от 0 до ![]() . Итак, для
. Итак, для ![]() , когда u=0, уравнение второго закона Кирхгофа
, когда u=0, уравнение второго закона Кирхгофа ![]() . Его решение
. Его решение![]() Постоянную интегрирования А определим из того, что в момент
Постоянную интегрирования А определим из того, что в момент ![]() ток в цепи, содержащей индуктивную катушку, не может измениться скачкообразно
ток в цепи, содержащей индуктивную катушку, не может измениться скачкообразно
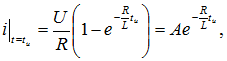
отсюда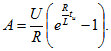 Подставляя значение А в уравнение (8.3), получим выражение тока при
Подставляя значение А в уравнение (8.3), получим выражение тока при ![]() :
: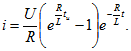 Выражение для напряжения на индуктивной катушке при
Выражение для напряжения на индуктивной катушке при ![]() :
: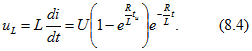
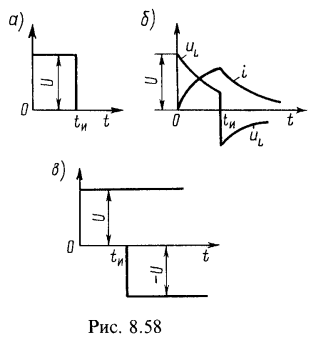
По уравнениям (8.1) (8.4) на рис. 8.58, б построены графики. Отметим, что в момент ![]() напряжение на индуктивной катушке изменяется скачком па величину, равную U. Скачок напряжения на индуктивности имеет место и при
напряжение на индуктивной катушке изменяется скачком па величину, равную U. Скачок напряжения на индуктивности имеет место и при ![]() .б. Принцип наложения. Прямоугольный импульс можно рассматривать как результат действия двух постоянных напряжений: напряжения U, включаемого в момент t=0 и действующего неограниченно долго, и отрицательного напряжения, равного — U, вступающего в действие в момент
.б. Принцип наложения. Прямоугольный импульс можно рассматривать как результат действия двух постоянных напряжений: напряжения U, включаемого в момент t=0 и действующего неограниченно долго, и отрицательного напряжения, равного — U, вступающего в действие в момент ![]() и также действующего неограниченно долго (рис. 8.58, в). Итак, для
и также действующего неограниченно долго (рис. 8.58, в). Итак, для ![]() ток определяют, как и раньше, по формуле (8.1).
ток определяют, как и раньше, по формуле (8.1).
Для ![]()
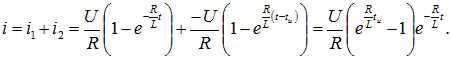
Смотри полное содержание по представленным решенным задачам.

