Магнитное поле (страница 2)

Магнитное поле (страница 2)

Магнитное поле (страница 2)
Магнитное поле стационарного тока в пустоте

1. Отрезок прямолинейного проводника с током (рис. 30) занимает часть оси Z от , до . Вычислите индукцию магнитного поля в точке М, лежащей в плоскости z=0.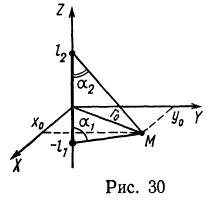Решение.
По определению



где r — вектор, проведенный от элемента dl до точки М.
Напоминая, что



и так как



для х-компоненты индукции получим



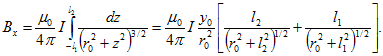
аналогично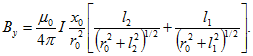 Тогда а) если
б) если
в) если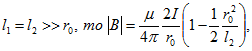
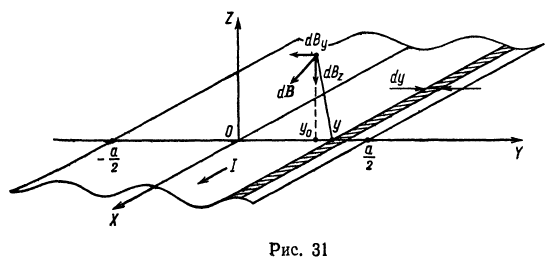
или так как , то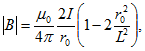 где L — полная длина проводника.2. По прямолинейной, бесконечно длинной и тонкой полоске шириной а течет постоянный ток I, равномерно распределенный по ее ширине. Вычислите индукцию магнитного поля и векторный потенциал в точках, лежащих на перпендикуляре к плоскости, проведенном через ее середину.

Решение.
Расположим систему отсчета так, как показано на рис. 31. Тогда (см. задачу 1.) компоненты индукции магнитного поля в точке с координатами , созданного узкой полоской, параллельной оси X, шириной dy и с координатой у, будут равны После интегрирования по у от -а/2 до а/2 получим Векторный потенциал А найдем из условия В=rot А.
Тогда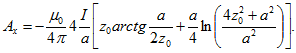 Примечания.
1) Наиболее интересными частными случаями являются случаи:
а) когда
б) когда
2) Можно определить в произвольной точке с координатами 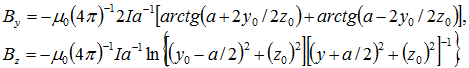3) При интегрировании были использованы табличные интегралы типа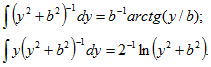

3. По тонкому проводнику, согнутому в виде окружности радиуса R, течет ток I. Механическая прочность проволоки . При каком значении индукции магнитного поля, перпендикулярного поверхности круга, произойдет разрыв проволоки.Решение.
На элемент проволоки dl с током I действует сила, равная



Проекция этой силы на выбранное направление (например, ось X), проходящее через центр окружности, равна



Следовательно сила, действующая на половину окружности,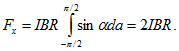 В момент разрыва . Поэтому .4. На деревянный круглый цилиндр объемом V в один слой намотана катушка, образующая короткий соленоид. По катушке течет ток, поверхностная плотность которого равна . Определите механический момент, который удерживает цилиндр в равновесии, если он находится во внешнем однородном поле с индукцией образующем угол a с осью цилиндра.Решение.
На катушку длиной dl действует со стороны внешнего поля вращающий момент, равный Полный момент будет равен . В условиях равновесия внешний момент . МАГНЕТОСТАТИКА МАГНЕТИКОВ5. «Жесткий» ферромагнетик (постоянный магнит), имеющий форму цилиндра радиуса R и высотой l однородно намагничен (M=const) в направлении оси цилиндра. Вычислите индукцию магнитного поля, созданного намагниченным ферромагнетиком в точках на оси цилиндра, если его вектор намагниченности равен М. Для точек внутри цилиндра найдите также значение вектора напряженности магнитного поля.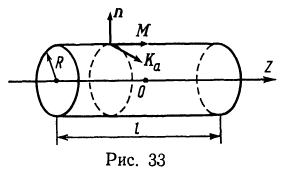Решение. Магнитное поле ферромагнетика мы найдем, если нам будет известно распределение объемного и поверхностного «тока Ампера», которое определяется соотношениями (рис. 33): где — значения вектора намагниченности по разные стороны поверхности, n — единичный вектор внешней нормали к поверхности.
Для рассматриваемого ферромагнетика в силу его однородной поляризации (M=const) в то время как на боковой поверхности цилиндра (внешняя среда считается вакуумом и поэтому ).
Таким образом, мы пришли к задаче о поле на оси цилиндрического проводника, по поверхности которого течет поверхностный ток . В ней мы приводим только результаты решения, заменяя на — полный ток.
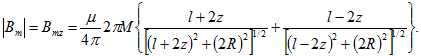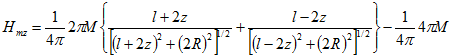В произвольной точке на оси цилиндра По определению Поэтому для и для (так как в этом случае М=0) т. е. вне ферромагаетика вектор напряженности и вектор индукции магнитного поля совпадают с точностью до постоянного множителя , а внутри ферромагнетика они антипараллельны.6. В однородное магнитное поле с индукцией внесли шарик радиуса R из магнетика, восприимчивость вещества которого — постоянная величина. Определите индукцию и напряженность магнитно поля в пространстве, окружающем шарик, и внутри шарика.Решение. Для шарика (эллипсоида) во внешнем однородном магнитном поле поляризация (намагничение) однородна. Поэтому в силу изотропности формы шарика, связь между остается векторной (фактор формы N — скаляр, для шара N= 1/3). Поэтому внутри шара По определению и условию задачи
Отсюда следует, что Поле вне шара является суперпозицией однородного поля и ноля, расположенного в центре шара диполя с магнитным моментом А так как , то , где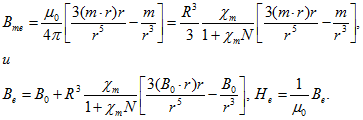 Из записанных выше соотношений вытекают формулы, которые полезно помнить: 7. Достаточно длинный цилиндрический соленоид радиуса R имеет однослойную обмотку. На каком расстоянии от одного из концов соленоида маленький парамагнитный шарик, расположенный на оси соленоида, будет испытывать максимальную силу?Решение. Индукция магнитного поля вблизи торда полубесконечного соленоида равна.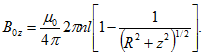 Для маленького парамагнитного шарика поле квази-однородно, поэтому где V — объем шарика, а — восприимчивость тела, и — восприимчивость вещества; фактор формы равен 1/3. Тогда Учитывая, что получим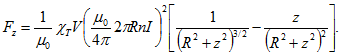 Так как при и , имеем
Что дает .

Смотри полное содержание по представленным решенным задачам.