Законы Кирхгофа в операторной форме

Рассмотрим rLC-цепь (рис. 15.1), которая была подключена к источнику ЭДС и в момент t = 0 переключается к источнику ЭДС e(t).

Дифференциальное уравнение цепи после коммутации

где напряжение и ток при выбранных положительных направлениях (рис. 15.1) связаны соотношениями

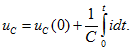
Рис. 15.1

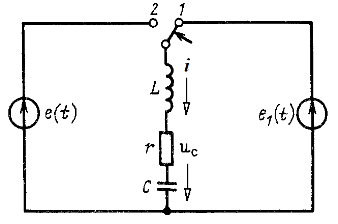
Напряжение , а также ток i(0), как и при расчете переходного процесса классическим методом, должны быть определены расчетом режима цепи до. коммутации, т. е. при действии источника ЭДС .

Перейдем в (15.15) от оригиналов к изображениям. С учетом (15.5), изображения постоянной величины (15.8) и (15.7) получим алгебраическое уравнение

где .

Из (15.16) определим ток:

Заметим, что в соответствии со сказанным выше нужно было бы писать . Но так как ток в индуктивности и напряжение на емкости не изменяются скачком при t = 0, будем писать короче: .

Выражение, стоящее в знаменателе, назовем полным сопротивлением rLC-цепи в операторной форме или операторным сопротивлением:

Сопротивление в операторной форме уже встречалось в разделе и теперь получено вполне строго. Напомним, что сопротивление rLC-цепи в операторной форме построено так же, как и комплексное сопротивление, если в последнем заменить через р. Величина, обратная операторному сопротивлению, называется операторной проводимостью:

Операторная ЭДС цепи, стоящая в числителе (15.17), состоит не только из операторного изображения ЭДС источника, т. е. Е(р), но и еще из двух слагаемых, которые определяются начальными условиями, т. е. током в индуктивности и напряжением на емкости . Иными словами, наличие двух дополнительных ЭДС , которые можно назвать внутренними или расчетными ЭДС, указывает на то, что в магнитном поле катушки и в электрическом поле конденсатора в момент коммутации была запасена энергия. Положительное направление ЭДС Li(0) совпадает с положительным направлением тока ветви, а направление ЭДС противоположно направлению тока. При этом, как и ранее, положительные направления тока и напряжения на конденсаторе считаются совпадающими. Например, при синусоидальной ЭДС , изображение которой , для тока получим изображение

т. е. рациональную дробь (15.9), у которой корни уравнения определяют установившуюся составляющую тока (синусоидальный ток), а корни уравнения , т.е. согласно (15.18) Z(p) = 0-характеристического уравнения последовательного контура, и определяют свободную составляющую тока.

Особенно просто выглядит выражение (15.17) при нулевых начальных условиях, т. е. при :

I(p) = E(p)/Z(p) (15.19)

оно аналогично закону Ома в комплексной форме.

Для любого узла разветвленной цепи

поэтому, обозначив изображения токов , на основании (15.1) получим первый закон Кирхгофа в операторной форме:

причем некоторые из токов могут быть изображением токов источников тока.

Для любого замкнутого контура, состоящего из n ветвей,

Переходя к изображениям, получаем второй закон Кирхгофа в операторной форме:

что можно переписать и так:

В последних выражениях - начальные значения токов в катушках индуктивности и напряжений на конденсаторах в соответствующих ветвях.

Особенно просто запишется второй закон Кирхгофа при нулевых начальных условиях, т. е. при :

он полностью аналогичен второму закону Кирхгофа в комплексной форме.

Итак, закон Ома, первый и второй законы Кирхгофа в операторной форме аналогичны по форме записи тем же законам в комплексной форме. Нужно только иметь в виду, во-первых, что в каждой k-й ветви при ненулевых начальных условиях, т. е. при , действуют не только внешняя ЭДС , но еще и внутренние ЭДС , и, во-вторых, что в качестве сопротивления ветви берется ее операторное сопротивление.

Изображение каждого из токов системы уравнений (15.22), так же как и тока в цепи на рис. 15.1, получается в виде (15.9) - отношения двух полиномов с действительными коэффициентами. При этом предполагается, что рассматриваются, как и ранее, линейные цепи с сосредоточенными параметрами, в которых действуют источники ЭДС (и тока), изображения которых записываются в виде отношения полиномов (например, постоянные, синусоидальные и экспоненциальные ЭДС, единичный скачок и единичный импульс).

Если изображение равно сумме нескольких рациональных дробей ( 15.9), то теорема разложения применяется отдельно к каждой из дробей.

Отношение изображений искомой величины к заданной называется передаточной или схемной функцией в операторной форме К (р), причем и составляется так же, как для цепей переменного тока .

Так как корни характеристического уравнения цепи зависят только от ее топологии и параметров, то их можно найти, сделав предположение, что в цепи действует только один источник ЭДС. Наиболее простое изображение имеет единичный импульс . При действии такой ЭДС изображение тока в ветви с источником

где - входное операторное сопротивление цепи относительно выводов источника. Входное операторное сопротивление составляется так же, как входное комплексное сопротивление, т. е. . Из (15.23) следует, что уравнение - это характеристическое уравнение цепи, на что было указано в разделе.

Аналогично можно показать, что, приравняв нулю входную проводимость цепи относительно двух ее любых узлов , также получаем характеристическое уравнение.

Дополнительно по теме