Расчет цепей при несинусоидальных периодических воздействиях и их коэффициенты

Расчет цепей при несинусоидальных периодических воздействиях и их коэффициенты

Расчет цепей при несинусоидальных периодических воздействиях и их коэффициенты, характерезующие форму

1. К зажимам цени (рис. 7.7), параметры которой , приложено напряжение
Частота основной гармоники . Написать выражения мгновенных значений тока i, напряжения на участке ab. Определить показания приборов, если — приборы магнитоэлектрической системы без выпрямления показывают среднее значение, — приборы индукционной системы — показывают действующее значение переменной составляющей, — приборы тепловой системы — показывают действующее значение тока и напряжения. Вычислить активную мощность, расходуемую в цепи.Решение:
Постоянные составляющие тока и напряжения на участке ab:

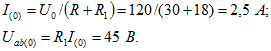Расчет для первой гармоники: Напряжение на участке ab

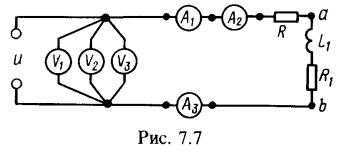
Расчет для третьей гармоники: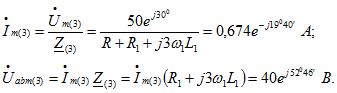 Уравнения для : 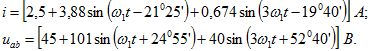Найдем показания приборов:
амперметр
вольтметр
амперметр
вольтметр
амперметр
вольтметр
Мощность, расходуемую в цепи, определяют

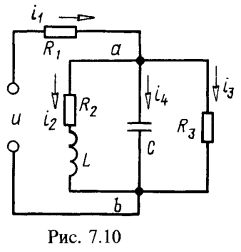
2. На рис. 7.10 изображена схема цепи, параметры которой при основной частоте имеют значения , а резистивные сопротивления: . Приложенное к цепи напряжение , где .
Записать уравнение мгновенного значения тока неразвствленного участка цепи. Определить действующее значение каждого тока. Вычислить мощность, расходуемую в цепи.

Решение:
Расчет постоянной составляющей. Эквивалентное сопротивление цепи и постоянные составляющие токов в неразветвленной части цепи и в ветвях с сопротивлениями определяют по формулам

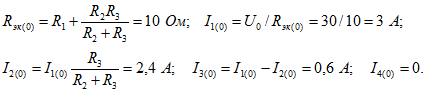Расчет для первой гармоники. Определим комплексное сопротивление трех параллельных ветвей отсюда Комплексное сопротивление всей цепи Комплексные (максимальные) токи в неразветвленной части цепи, напряжение на параллельных ветвях и токи в них: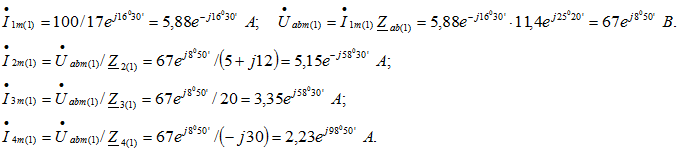 Расчет для третьей гармоники проводится аналогично: 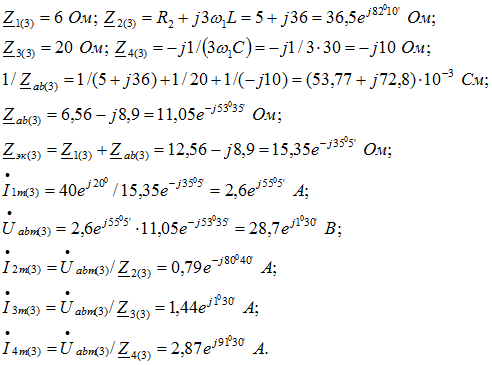Ток в неразветвленной части цепи имеет вид Действующее значение каждого тока определяют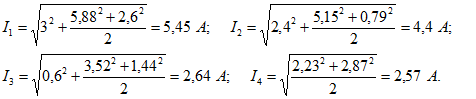 Мощность, расходуемую в цепи, находят по формуле Проверка 3. Вычислить коэффициенты формы, амплитуды и искажения кривой напряжения, уравнение которой: Решение:
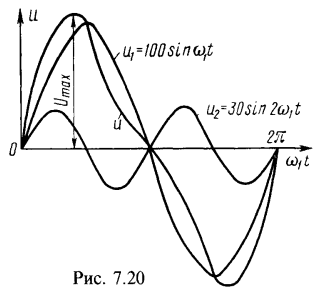
Сначала вычислим действующее значение напряжения по формуле: Затем найдем среднее по модулю значение напряжения. Ввиду симметрии кривой u и положительности ее значений за половину периода (рис. 7.20) для его определения достаточно ограничиться половиной периода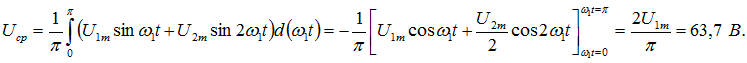

Теперь определим максимальную ординату кривой u:

или так как , то , откуда, решая квадратное уравнение, получим

(знак « —» перед корнем не ставят, так как в этом случае косинус окажется больше единицы), a.Наконец, по формулам вычислим искомые коэффициенты:

4. Найти коэффициенты формы, амплитуды и искажения кривой напряжения
.Решение:

Смотри полное содержание по представленным решенным задачам.