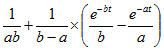Расчет переходных процессов. Операторные схемы замещения. Использование теоремы разложения

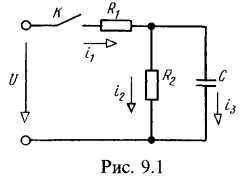
1. Для схемы рис. 9.1 операторным методом найти выражения мгновенных значений тока в неразветвленной части цепи и напряжения на обкладках конденсатора при замыкании контакта К. Дано:
Решение:
Находим изображение тока в неразветвленной части цепи по закону Ома: , где изображение постоянного напряжения (см. по табл. 0.9.1, № 2) , а операторное сопротивление

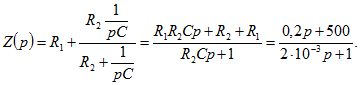Итак,

Оригинал этого тока определим двумя способами.Способ 1. Используя таблицу 0.9.1 (смотри внизу), связывающую оригинал и его изображение, преобразуем так, чтобы получить табличные изображения.
представим в виде суммы двух функций, которые после преобразования примут вид формул, данных в табл. 0.9.1, № 5 и 11: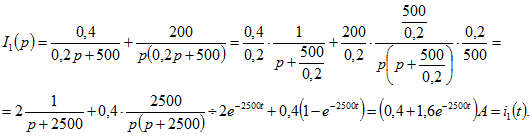
Способ 2. Решим задачу с помощью теоремы разложения [см. формулу (0.9.11), представлена ниже]
В данном случае:
Вычисляем корень уравнения:
Определяем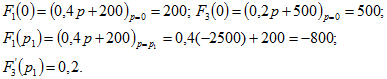 Подставляя найденные значения в формулу, получим
Проверка. При , ток . Действительно, в момент начала переходного процесса напряжение на конденсаторе равно нулю. Это соответствует тому, что конденсатор ведет себя так, будто он закорочен, и тем самым шунтирует сопротивление , поэтому ток определяется только сопротивлением . Определим напряжение на конденсаторе в операторной форме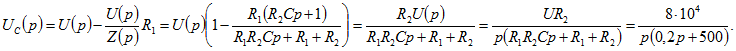 Применяя один из указанных способов, найдем Проверка. При напряжение , что соответствует начальному условию. 2. Решить задачу №1 предыдущего раздела операторным методом.Решение:
Прежде всего найдем операторное сопротивление цепи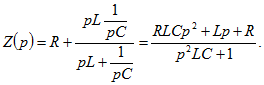 Далее определим изображение тока через изображение входного напряжения : Изображение напряжения на конденсаторе получим, умножая изображение тока на операторное сопротивление параллельных ветвей: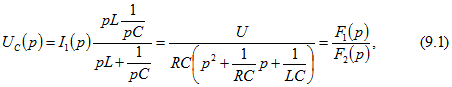 где числитель а знаменатель причем корни уравнения 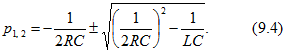1. Решим задачу для первого варианта числовых значений по формуле разложения (0.9.10). По формулам (9.2) - (9.4) определяем 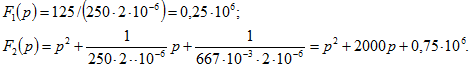Найдем корни уравнения: 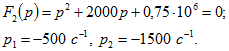Вычислим производную и ее значения при и : По формуле (9.1) определяем По формуле разложения, Те же результаты можно получить по формуле табл. 0.9.1, № 13, если знаменатель изображения напряжения на конденсаторе представить в виде .2. Решим задачу, подставляя числовые значения второго варианта. По формулам (9.2) - (9.4) определим Изображение напряжения на конденсаторе [см. формулу 9.1)] имеет вид В связи с тем, что имеются кратные корни (порядок кратности m=2), оригинал находим по формуле (0.9.12), в которой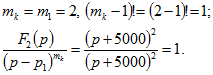 Таким образом,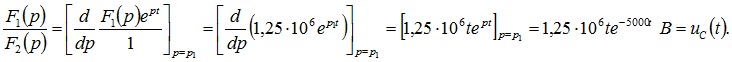
Можно также определить оригинал по формуле табл. 0.9.1, № 9.3. Рассмотрим третий вариант числовых значений. По формулам (9.2) — (9.4) находим

Производная от и ее значения при и равны: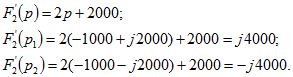 Искомый оригинал имеет вид [см. формулу 0.9.10]: 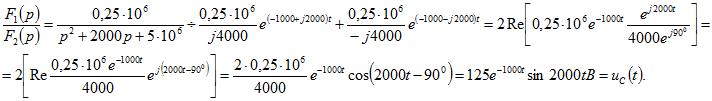Те же результаты можно получить по формуле табл. 0.9.1, № 18, если знаменатель представить в виде

3. Решить задачу №3 предыдущего раздела операторным методом.Решение:
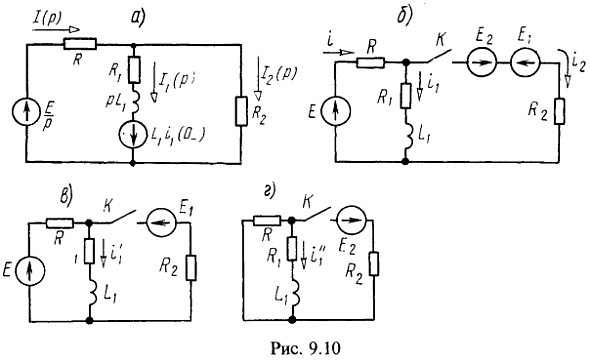
Это пример задачи с ненулевым начальным условием для тока , проходящего через индуктивную катушку. Операторная схема замещения изображена на рис. 9.10, а. Составляем для нее уравнения Кирхгофа: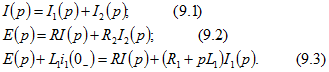 В этих уравнениях — начальное значение тока, проходящего через индуктивную катушку — изображение постоянной ЭДС.
Уравнения (9.1) — (9.3) решим совместно относительно тока : 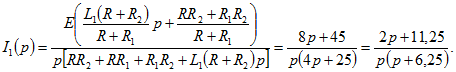По формуле разложения (0.9.11) оригинал функции имеет вид Для упражнения эту же задачу решим методом сведения к нулевым начальным условиям. Для этого вычислим напряжение на разомкнутом контакте (см. рис. 8.9, а): Добавим в ветвь два встречно включенных источника с ЭДС , как показано на рис. 9.10, б.
Расчет схемы после коммутации проведем по методу наложения. Составляющая тока (от системы ) совпадает со своим значением до коммутации, так как подключение ЭДС (рис. 9.10, в) не вызовет каких-либо изменений в исходной схеме с выключенным контактом К. Таким образом, .
Вызываемую действием ЭДС подключаемой к обесточенной схеме (рис. 9.10, г), составляющую тока можно записать в операторной форме: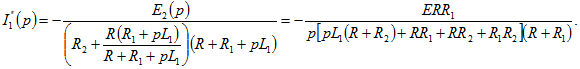 Подставляя числовые значения и переходя к оригиналу для искомого тока, получим

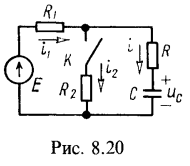
4. Определить операторным методом напряжение на конденсаторе и токи при замыкании контакта К (рис. 8.20). Дано: Е=24 В, R=20 Ом, С=3 мкФ.Решение:
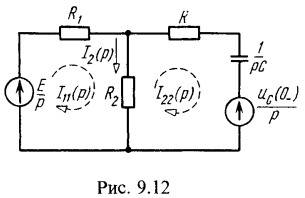
Эта задача имеет ненулевое начальное условие для напряжения на конденсаторе . Операторная схема замещения изображена на рис. 9.12.
Для этой схемы по методу контурных токов имеем

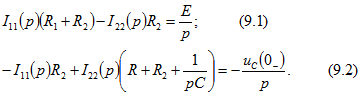Решая эти уравнения относительно и учитывая, что , найдем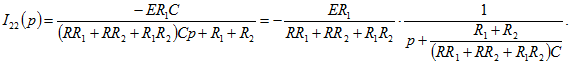
Подставив числовые значения, получим На основании (0.9.10) или по табл. 0.9.1, № 5 определим оригинал: Аналогично из уравнений (9.1) и (9.2) можно наши другие токи и напряжение на конденсаторе.

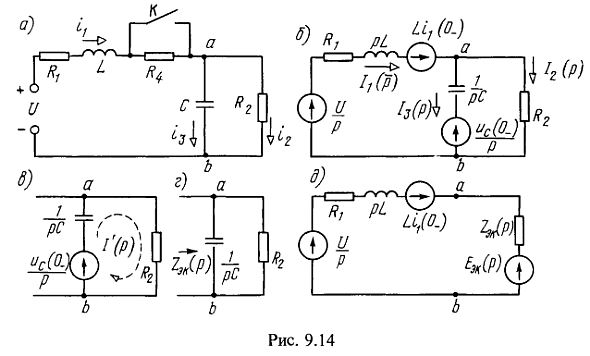
5. В схеме (рис. 9.14, а) при разомкнутом контакте имеется установившийся процесс. В момент t=0 контакт замыкается и накоротко шунтирует сопротивление .
Найти выражения для токов и напряжение на конденсаторе при переходном процессе. Дано:
Решение:
Это пример задачи с ненулевыми начальными условиями. Определим их. Через индуктивную катушку до замыкания контакта проходит постоянный ток Напряжение на конденсаторе до коммутации:
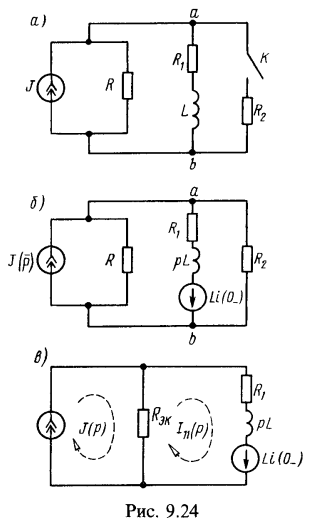
Для схемы, образующейся после коммутации, начертим операторную схему замещения (рис. 9.14, б). Найдем, например, ток методом эквивалентного источника ЭДС. Для этого отключаем первую ветвь (рис. 9.14, в) и найдем операторную ЭДС эквивалентного источника и его сопротивление . Из рис. 9.14, в следует, что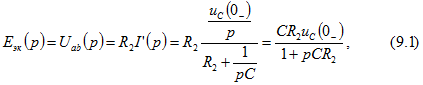

а из рис. 9.14, г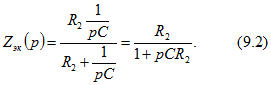

Ток в первой ветви (рис. 9.14, д)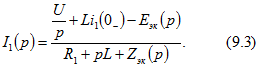
Подставим сюда из (9.1) и (9.2), получим Подставляя числовые значения, имеем: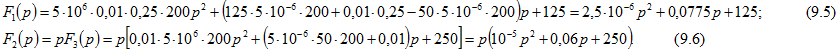 По изображению (9.14) найдем оригинал тока с помощью теоремы разложения. Для этого определим значения функции при р=0. Зачем находим корни уравнения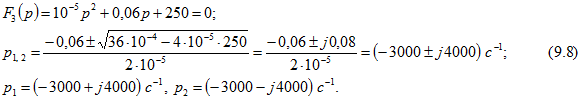 Далее вычислим производную и ее значения при 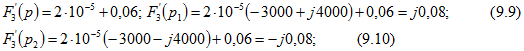Определим при 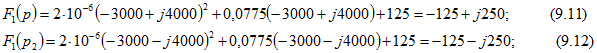Наконец, подставим полученные в уравнениях (9.7)-(9.12) значения в формулу (0.9.11) и, учитывая замечание теоремы разложения, определяем 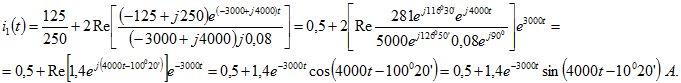Проверка. При , что удовлетворяет начальному условию.
Остальные два тока могут быть найдены следующим образом. Если из U вычесть падение напряжения на ветви , то можно найти мгновенное значение напряжения на параллельных ветвях: Затем определим токи:

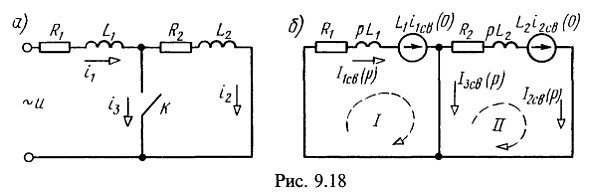
6. К зажимам цепи (рис. 9.18, а) приложено напряжение . Параметры цепи: .
В момент прохождения тока через положительный максимум замыкается контакт К. Найти токи .Решение:
До замыкания контакта ток в цепи где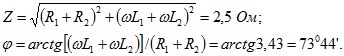 По условию задачи в момент включения этот ток максимален, т. е.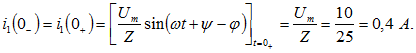
Отсюда можно рассчитать угол включения y:

Так как изображение синусоидальной функции определяется сравнительно сложной формулой, в данной задаче операторным методом вычислим только свободную составляющую тока , а установившуюся составляющую тока найдем, рассчитав схему задачи (см. рис. 9.18, а) после коммутации символическим методом 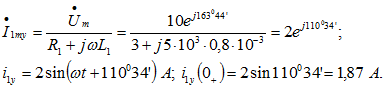Начальное значение свободного тока:
Операторная схема замещения для расчета свободной составляющей переходного процесса с учетом ненулевых начальных значений свободных токов показана на рис. 9.18, б.
По второму закону Кирхгофа для первого контура имеем: и, подставляя числовые значения и вычисляя изображение свободного тока, находим По формуле разложения: . Суммирование установившегося и свободного токов определяет искомый ток: .
Аналогично вычисляем ток . Отличие заключается в том, что установившийся ток равен нулю:
Поэтому . По второму закону Кирхгофа, для второго контура (рис. 9.18, б) По формуле разложения:

7. Цепь, состоящая из источника постоянного тока , нагруженная на - ветвь, находится в установившемся режиме (рис. 9.24, а). В момент t=0 замыканием контакта К осуществляется коммутация, включающая резистор сопротивлением . Найти закон изменения тока , протекающего через ветвь после замыкания.Решение:
До коммутации по ветви проходил постоянный ток: .
Начертим эквивалентную операторную схему замещения после коммутации (рис. 9.24, б) и заменим ее схемой рис. 9.24, в, в которой параллельно соединенные сопротивления заменим эквивалентным: . По методу контурных токов имеем . Отсюда, учитывая, что найдем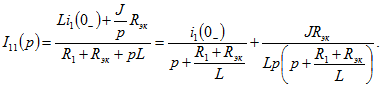
Используя таблицу 0.9.1, № 5 и 11, найдем оригинал каждого из этих изображений. В результате получим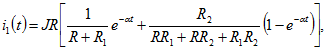 где

ОСНОВНЫЕ ПОЛОЖЕНИЯ И СООТНОШЕНИЯ

1. Преобразование Лапласа. В основу операторного метода положено следующее. Функция [обычно ток или напряжение ] вещественного переменного (время), называемая оригиналом, заменяется соответствующей ей функцией комплексного переменного , называемой изображением.
Эти функции связаны соотношением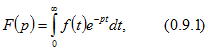 называемым прямым преобразованием Лапласа. Сокращенно эту связь записывают в таком виде: .
В табл. 0.9.1 приводятся оригиналы простейших функций и их изображения, полученные по формуле (0.9.1) и используемые при решении задач на переходные процессы.

Таблица 0.9.1


№ п/п	Оригинал	Изображение	№ п/п	Оригинал	Изображение
1			12
2			13
3			14
4			15
5			16
6			17
7			18
8			19
9			20
10			21
11			22
n — целое положительное число В таблице для сокращения записи под каждой из функций оригиналов f(t) следует понимать f(t) 1(f).

2. Теорема разложения. Если изображение искомого тока или напряжения имеет вид рациональной дроби причем многочлены (относительно ) удовлетворяют следующим условиям: степень ниже степени — вещественные числа, а корни уравнения различны, то оригинал определяется выражением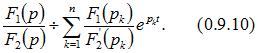 Если знаменатель уравнения имеет один корень, равный нулю, т. е. , то оригинал находят по формуле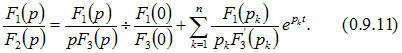 Замечание. Если среди корней уравнения имеются комплексно-сопряженные корни , то при вычислении соответствующих им слагаемых, стоящих в правой части суммы уравнений (0.9.10) и (0.9.11), достаточно определить слагаемое для одного из этих корней, например для сопряженного корня следует взять сопряженное значение этого слагаемого. Сумма, соответствующая этим двум слагаемым, равна удвоенному значению действительной части, найденной для одного из корней. Если в уравнении (0.9.11) имеет различных корней и из них корень кратностью , корень кратностью т2, корень рп кратностью , то по изображению оригинал вычисляют по формуле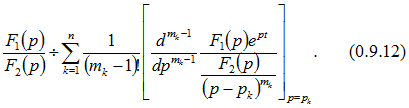 Здесь выражение, стоящее в знаменателе квадратной скобки, надо сначала сократить на и лишь после этого дифференцировать.
Если уравнение содержит одновременно и простые, и кратные корни, то для определения слагаемых, соответствующих простым корням, используется формула (0.9.10) или (0.9.11), если имеется простой корень , а для кратных - формула (0.9.12).

Смотри полное содержание по представленным решенным задачам.