Баланс мощностей для простой неразветвленной цепи
Баланс мощностей для простой неразветвленной цепи
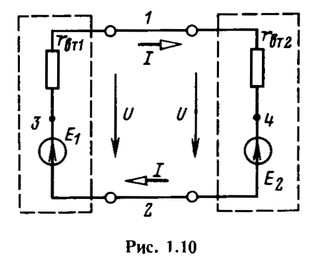
Рассмотрим энергетические соотношения для электрической цепи, состоящей, например, из одной машины постоянного тока с ЭДС Е1 и внутренним сопротивлением rвт1 и аккумуляторной батареи с ЭДС Е2 и внутренним сопротивлением rвт2 (рис. 1.10). ЭДС машины и аккумуляторной батареи направлены навстречу друг другу. Пусть ЭДС Е1 машины больше ЭДС Е2 аккумуляторной батареи. При этом условии действительное направление тока I совпадает с направлением ЭДС E1. Напряжение U на выводах обоих источников меньше ЭДС E1 на внутреннее падение напряжения rвт1I в машине и больше ЭДС Е2 на падение напряжения rвт2I в батарее.
Действительно, по ( 1.11а)
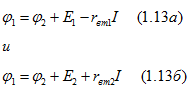
так как ![]() . Напряжение
. Напряжение ![]() , поэтому
, поэтому
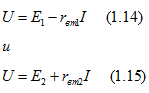
После умножения обеих частей (1.14) на I и перестановки слагаемых получаем
![]()
Левая часть этого уравнения представляет собой мощность, развиваемую машиной; первое слагаемое правой части определяет мощность тепловых потерь (в обмотке машины), а второе слагаемое правой части - мощность, отдаваемую машиной аккумуляторной батарее.
Умножив правую и левую части выражения (1.15) на ток I, получим
![]()
Дополнительно по теме
- Элементы электрических цепей и схем
- Схемы замещения источников энергии
- Закон Ома для участка цепи с ЭДС
- Баланс мощностей для простой неразветвленной цепи
- Законы Кирхгофа и их применение
- Топологические графы
- Законы Кирхгофа в матричной форме
- Метод узловых потенциалов
- Метод контурных токов
- Уравнения цепи в матричной форме
- Расширенные узловые уравнения
- Преобразования в линейных электрических схемах
Из этого уравнения непосредственно вытекает, что мощность UI, получаемая аккумуляторной батареей, состоит из мощности тепловых потерь ![]() и мощности, необходимой для зарядки аккумуляторов
и мощности, необходимой для зарядки аккумуляторов ![]() .
.
Полученные соотношения для баланса мощностей применимы не только к цепи зарядки аккумуляторов, но и к любым другим цепям. Отличие состоит лишь в том, что в приемниках другого рода электрическая энергия расходуется не на зарядку аккумуляторов, а на другие процессы, например в электрических двигателях - на механическую работу, в резисторах - только на тепловые потери.
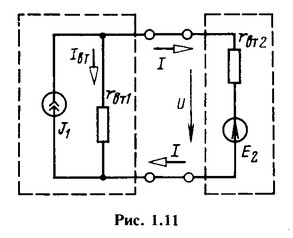
Если представить источник энергии другой эквивалентной схемой (рис. 1.11), то окажется, что мощность, развиваемая источником тока, не равна мощности, развиваемой источником ЭДС. Действительно, мощность, развиваемая источником тока, определяется произведением тока J1 и напряжения U на выводах источника тока, т. е. равна J1U. Так как ![]() , то после замены тока J1 и простых преобразований получим
, то после замены тока J1 и простых преобразований получим
![]()
Из сравнения выражений (1.18) и (1.16) непосредственно следует, что при одинаковом напряжении на выводах обоих источников и одинаковом токе I тепловые потери ![]() при схеме по рис. 1.10 не равны в общем случае тепловым потерям
при схеме по рис. 1.10 не равны в общем случае тепловым потерям ![]() при схеме по рис. 1.11, вследствие чего и мощность, развиваемая источником ЭДС Е1I, не равна мощности, развиваемой источником тока J1U. Это следует иметь в виду при замене реального источника энергии источником ЭДС или источником тока.
при схеме по рис. 1.11, вследствие чего и мощность, развиваемая источником ЭДС Е1I, не равна мощности, развиваемой источником тока J1U. Это следует иметь в виду при замене реального источника энергии источником ЭДС или источником тока.
Пример 1.1.
К выводам последовательно соединенных источников энергии (ЭДС E1=12 В и Е2 = 48 В; внутренние сопротивления rвт1 = 0,4 Ом и rвт2 = 0,6 Ом) подключен приемник - резистор с изменяющимся сопротивлением (рис. 1.12). Определить значение сопротивления r, при котором мощность резистора максимальна. Найти мощность приемника и источников энергии при этом значении сопротивления.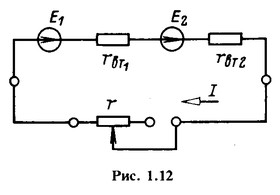
Решение.
Для определения сопротивления r, при котором мощность резистора максимальна, воспользуемся выражением мощности ![]() .
.
Так как ток
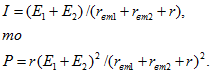
Вычислив производную от Р по r и приравняв ее нулю, найдем искомое сопротивление
![]()
Это соотношение показывает, что мощность приемника максимальна при равенстве суммарного внутреннего сопротивления источников и сопротивления приемника.
Значения остальных величин определяются но формулам:
ток
![]()
мощности, развиваемые первым и вторым источниками ЭДС,
![]()
мощность приемника
![]()
мощность тепловых потерь в обоих источниках
![]()
т. е. мощность приемника равна мощности потерь в обоих источниках (так как мощность резистора максимальна при ![]() ).
).
Смотри ещё по теме Электрические цепи постоянного тока
Основные законы и методы расчета электрических цепей постоянного тока
- Элементы электрических цепей и схем
- Схемы замещения источников энергии
- Закон Ома для участка цепи с ЭДС
- Баланс мощностей для простой неразветвленной цепи
- Законы Кирхгофа и их применение
- Топологические графы
- Законы Кирхгофа в матричной форме
- Метод узловых потенциалов
- Метод контурных токов
- Уравнения цепи в матричной форме
- Расширенные узловые уравнения
- Преобразования в линейных электрических схемах
Основные свойства электрических цепей постоянного тока
- Принцип наложения (суперпозиции)
- Свойство взаимности
- Входные и взаимные проводимости, коэффициенты передачи
- Принцип компенсации. Зависимые источники
- Общие замечания о двухполюсниках и многополюсниках
- Линейные соотношения между напряжениями и токами
- Теорема о взаимных приращениях токов и напряжений
- Принцип эквивалентного генератора
- Передача энергии от активного двухполюсника к пассивному

