Численные методы решения уравнений состояния

Интегрирование дифференциальных уравнений, составленных методом переменных состояния в форме Коши ( 14.91), чаще выполняется численными методами на ЭВМ с применением программ. Интервал времени, в течение которого необходимо найти значения искомых величин, разделяется на малые равные (или неравные) промежутки - шаги , и в результате расчета получаются значения этих величин в отдельные (дискретные) моменты времени , где k = 1, 2, 3... Предполагается, что значения искомых величин в начальный момент времени известны (начальные условия задачи).

Математиками разработаны различные методы численного решения уравнений, записанных в форме Коши, из которых далее рассматриваются более простые - одношаговые. В одношаговых методах искомые величины в момент времени определяются по уже найденным значениям на предыдущем одном шаге.

Наиболее простой из одношаговых методов - явный метод Эйлера или алгоритм Рунге-Кутта первого порядка - записывается так:

где матрица-столбец переменных состояния для k-го шага; Xk-t - то же для (к - 1)-го шага (в момент tk-1); - матрица-столбец производных (точнее, угловых коэффициентов касательных) переменных состояния в момент (в начале предыдущего шага). Метод основан на разложении каждой переменной состояния в ряд Тейлора

и учете его первых двух членов. Метод назван явным, так как искомое решение для k-го шага не входит в правую часть алгоритма (14.101), связывающего значения на последующем и предыдущем шагах.

После подстановки (14.916), записанного для (k - 1)-го шага, в (14.101) получим

Формула (14.102) - это рекуррентное соотношение, которое дает возможность непосредственно определять последующие значения переменных состояния по найденным на предыдущем шаге. Чем меньше шаг h, тем точнее расчет, но больше объем вычислений. Погрешность расчета пропорциональна .

В алгоритмах Рунге-Кутта более высокого порядка искомые величины для k-го шага определяются с учетом их значений в нескольких промежуточных точках предыдущего (k - 1)-го шага, так что точность расчета увеличивается.

Если в правой части (14.101) производные для предыдущего (k - 1)-го шага заменить производными для данного k-го шага, то получим

Алгоритм называется неявным методом Эйлера, так как правая часть (14.103) содержит производные для того же шага, для которого определяются переменные состояния.

После подстановки ( 14.91 б), записанного для момента , в (14.103) получим

откуда

Погрешность расчета того же порядка, что и для явного метода Эйлера.

Лучшую точность обеспечивает метод трапеций (относится к неявным), так как в правой части содержит средние значения производных (k - 1)-го и k-го шагов:

После подстановки (14.916), записанных для моментов , в (14.105) получим

откуда

Погрешность расчета пропорциональна .

Полная погрешность зависит не только от выбранного метода расчета, т. е. от методической погрешности (алгоритмической), но и от погрешности округления из-за ограниченного количества разрядов цифровых значений величин, что относится, конечно, к любым расчетам электрических цепей.

С ростом числа шагов погрешность интегрирования может увеличиваться, т. е. численное решение может давать значения, все более отличающиеся от истинных. В этом случае получается численно неустойчивый алгоритм, который нельзя использовать для расчета переходного процесса. Устойчивость явного метода Эйлера зависит от шага к Для цепей с одним накопителем алгоритм получается устойчивым при , где - постоянная времени цепи. Для цепи с несколькими накопителями при действительных корнях характеристического уравнения необходимо выбрать , где - минимальный коэффициент затухания, а при наличии и комплексных корней шаг h должен быть еще и меньше минимального значения .

Неявный метод Эйлера и метод трапеций устойчивы при любом шаге. Поэтому выбор шага диктуется только необходимой точностью расчета, которая, однако, при уже выбранном шаге еще неизвестна, что относится и к явным методам.

Пример 14.7.

Для цепи примера 14.6 (рис. 14.42) сравнить результаты расчета тока явным методом Эйлера, неявным методом Эйлера и методом трапеций с данными аналитического расчета, приведенными в примере 14.6, при шаге h = 0,005 с.

Решение. Обозначим переменные состояния , так что .

Явный метод Эйлера. Согласно (14.102)

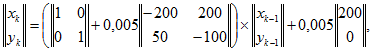
и после выполнения операций сложения и умножения матриц получим

Результаты расчета приведены в табл. 14.2.

Таблица 14.2

k	1	2	3	4	5	6	7	8	9	10
	1,000	1,250	1,375	1,500	1,594	1,672	1,734	1,785	1,826	1,859
k	11	12	13	14	15	16	17	18	19	20
	1,886	1,908	1,925	1,939	1,951	1,961	1,968	1,974	1,979	1,983

Неявный метод Эйлера. В (14.104) входит обратная матрица

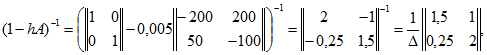
где . После подстановки матриц

в (14.104) получим

Результаты расчета приведены в табл. 14.3.

Таблица 14.3

k	1	2	3	4	5	6	7	8	9	10
	1,091	1,207	1,321	1,424	1,514	1,591	1,656	1,711	1,757	1,796
k	11	12	13	14	15	16	17	18	19	20
	1,823	1,856	1,879	1,899	1,911	1,928	1,940	1,950	1,958	1,964

Метод трапеций. В (14.106) входят матрицы

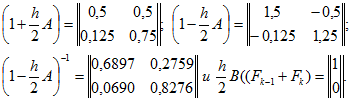
После подстановки этих матриц в (14.106) получим

Результаты расчета приведены в табл. 14.4.

Таблица 14.4

k	1	2	3	4	5	6	7	8	9	10
	1,070	1,209	1,342	1,456	1,551	1,629	1,694	1,747	1,792	1,828
k	11	12	13	14	15	16	17	18	19	20
	1,858	1,882	1,903	1,920	1,934	1,945	1,955	1,963	1,969	1,975

Сравнение значений тока рассчитанных аналитическим методом (см. табл. 14.1) и численными методами (табл. 14.2-14.4), показывает, что, как и должно быть, наиболее близкие к приведенным в табл. 14.1 значения тока получаются методом трапеций (отличие не более 1%, а начиная с k = 3 не более 0,2%).

Для устойчивых методов точность решения повышается при уменьшении шага h, однако при этом возрастает время решения и увеличивается погрешность, связанная с округлением результатов вычисления на ЭВМ, так как растет общее количество вычислений. Поэтому существующие стандартные программы решения дифференциальных уравнений снабжаются автоматическим выбором шага интегрирования: шаг увеличивается, если обеспечена заданная точность решения, в противном случае он дробится до тех пор, пока не будет достигнута заданная точность.

При решении задач с применением ЭВМ часто нецелесообразно разделять задачи по признаку установившихся и переходных процессов. Программа решения задачи в случае переходных процессов всегда по истечении определенного времени приводит к решению для установившегося режима. Поэтому все соображения по расчету с применением ЭВМ, приведенные в данном параграфе, в равной степени могут быть отнесены как к переходным, так и к установившимся процессам.

Дополнительно по теме