Пример классического метода

Смотреть теорию по разделу Общий случай расчета переходных процессов классическим методом

Пример 14.2. Найти ток в цепи на рис. 14.28 при параметрах Выбранные положительные направления токов и напряжения на конденсаторе показаны на рисунке.

Решение.

1) Дифференциальные уравнения цепи после коммутации

2) Независимые начальные условия

3) Искомый ток

4) После коммутации ток (замыкается в ветви с индуктивным элементом; источник ЭДС не создает тока в ветви с ЭДС так как ток второго источника тоже замыкается в ветви с индуктивным элементом).

5) Входное сопротивление для источника ЭДС, включаемого в ветвь с ключом,

Характеристическое уравнение имеет корни

6) Свободная составляющая тока при различных действительных корнях

7) Искомое решение записывается в виде

8) Для определения постоянных интегрирования составим систему уравнений

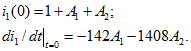
Для решения этой системы необходимо найти начальные значения тока и его производной из системы уравнений Кирхгофа с учетом независимых начальных условий. При t = 0

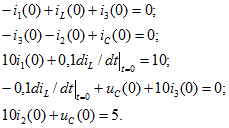
Рис. 14.28

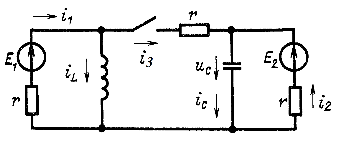
Так как уже найдены независимые начальные условия, то это система пяти алгебраических уравнений с пятью неизвестными. После решения находим

Для определения дифференцируем систему уравнений Кирхгофа и подставляем t = 0:

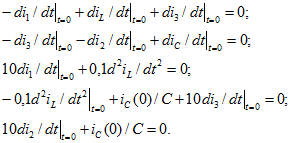
Здесь пять неизвестных, любую из которых можно найти. Чтобы вычислить производную , проще всего сложить третье и четвертое уравнения. Их сумма и первое уравнение - это два уравнения с двумя неизвестными, откуда находим Теперь из системы уравнений относительно определяем

9) Ответ:

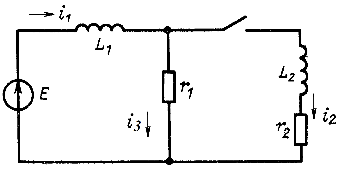
Пример 14.3. Для цепи на рис. 14.29 заданы параметры: Найти ток после коммутации.

Решение.

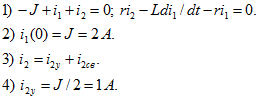
Входное сопротивление для источника ЭДС, включаемого в ветвь ключа (источник тока идеальный). Из характеристического уравнения находим

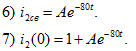
При t = 0 из первого уравнения Кирхгофа , т.е. А = - 1.

Рис. 14.29

Рассмотренный метод расчета переходных процессов применим и к цепям, схемы замещения которых содержат управляемые источники.

Пример 14.4.

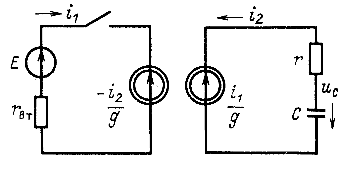
К выходным выводам гиратора присоединена rС-цепь Гиратор подключается к источнику с постоянной ЭДС Е и внутренним сопротивлением (рис. 14.30). Определить напряжение .

Решение.

Дифференциальные уравнения цепи

где

После исключения токов получим дифференциальное уравнение для напряжения

где

Начальное условие . Напряжение где (источник постоянной ЭДС), т. е., как следует из уравнения, . Свободная составляющая где корень находится из характеристического уравнения , т.е. . Так как , то

Рис. 14.30

Дополнительно по теме