+7 (351) 215-23-09


Символический метод расчета цепей переменного тока



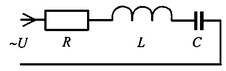
Соединим последовательно лампу накаливания с сопротивлением R, батарею конденсаторов с емкостью С и катушку с большой индуктивностью L. Если данную цепь присоединить к зажимам генератора переменного тока, то лампа загорится, что свидетельствует о наличии электрического тока в цепи, несмотря на разрыв, существующий между изолированными друг от друга обкладками конденсатора.

Для цепи переменного тока с последовательным соединением R, L, С (см. рисунок) дифференциальные уравнения по второму закону Кирхгофа имеют вид:

Здесь ток во всех трех участках один и тот же:

Разности потенциалов на всех трех сопротивлениях имеют вид:

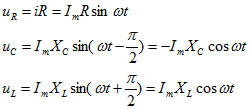
Решение системы дифференциальных уравнений можно существенно упростить, если перейти от дифференциальных уравнений к алгебраическим. Это можно сделать, изображая синусоидальные величины (i, u) в комплексной форме, т.е. в виде вектора на комплексной плоскости.

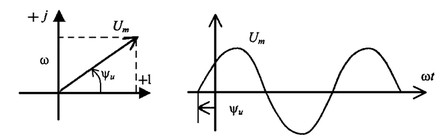
Вектор Um и его проекции

Расположим под углом относительно оси абсцисс вектор Um, длина которого в масштабе равна амплитуде изображаемой величины. Положительные углы будем откладывать в направлении против часовой стрелки.

Проекции вектора на вертикальную ось мнимых величин в комплексной плоскости равны мгновенному значению напряжения.

Система векторов на комплексной плоскости называется векторной диаграммой. Вектора вращаются относительно центра координат с одной и той же скоростью и поэтому относительно друг друга их положение не меняется. Векторная диаграмма изображается неподвижной в заданный момент времени, определяемый начальной фазой какой-либо величины, например, для идеальных элементов R, L, С.

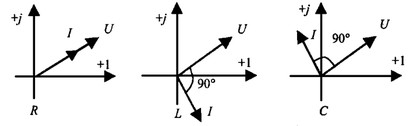
Векторные диаграммы для идеальных элементов R, L, C

Сложение двух функций в тригонометрической форме трудоемко, но легко производится в векторной форме.

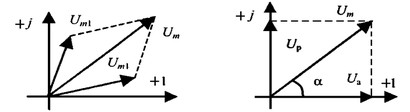
Векторные диаграммы сложения двух напряжений

В расчетах применяют три формы записи комплексных величин:

  1. алгебраическая

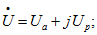
  2. тригонометрическая

  3. показательная, учитывая

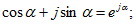
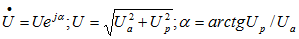
Символ j перед мнимой частью комплексного числа в алгебраической форме означает, что мнимая часть повернута по отношению к вещественной на угол 90° в положительном направлении (против часовой стрелки).

Переходы из одной формы записи в другие:

где

где

Представленная ранее система дифференциальных уравнений для цепи переменного тока с R, L, С в комплексном виде записывается следующим образом:

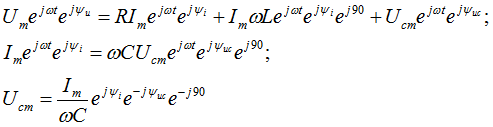
Используя выражения , запишем выражение для полного напряжения цепи:

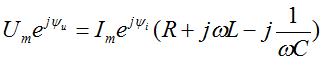
где

- комплексное сопротивление;

- комплексная амплитуда напряжения;

- комплексная амплитуда тока.

При замене амплитудных значений на действующие получим закон Ома в комплексной форме:

Величину Z называют полным сопротивлением цепи переменного тока.

Первый закон Кирхгофа в комплексной форме:

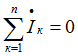
Второй закон Кирхгофа в комплексной форме:

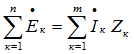
Векторная диаграмма напряжений для цепи с последовательным соединением R, L, C будет представлять собой прямоугольный треугольник.

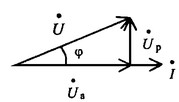
Треугольник напряжений

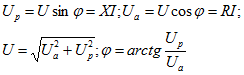
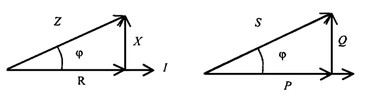
Треугольники токов, сопротивлений и мощностей строятся аналогично

Полная мощность S = UI;

активная мощность

реактивная мощность

где

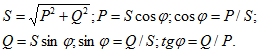
В треугольниках напряжений, токов, сопротивлений и мощностей угол сохраняет свое значение.

При параллельном соединении ветвей их проводимости складываются в комплексной форме:

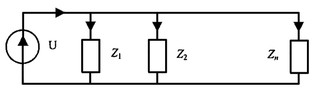
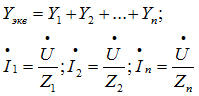
Общий ток, согласно первому закону Кирхгофа:

Дополнительно по теме