Резонанс в параллельном контуре

Рассмотрим цепь с двумя параллельными ветвями: параметры одной - сопротивление и индуктивность L, а другой - сопротивление и емкость С (рис. 5.5). Такую цепь часто называют параллельным контуром. Резонанс наступает, если у входной проводимости

реактивная составляющая

или

где

- реактивные проводимости ветвей.

При противоположные по фазе реактивные составляющие токов равны (рис. 5.6, а), поэтому резонанс в рассматриваемой цепи получил название резонанса токов. Из векторной диаграммы видно, что при резонансе ток I на входных выводах контура может быть значительно меньше токов в ветвях.

Дополнительно по теме

Рис. 5.5

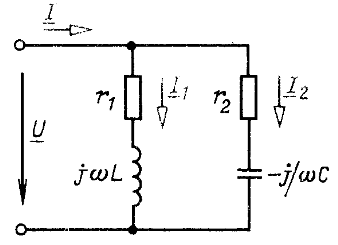
Рис. 5.6

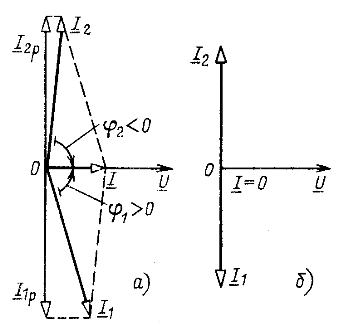
В теоретическом случае при токи и сдвинуты по фазе относительно напряжения на углы и (рис. 5.6, б) и суммарный ток . Входное сопротивление цепи при этом бесконечно велико.

Подставив в соотношение (5.12), т. е. в условие резонанса, значения и , выраженные через параметры цепи и частоту, получим

Изменением одной из величин () при остальных четырех постоянных не всегда может быть достигнут резонанс. Резонанс отсутствует, если значение изменяемой величины при ее определении из уравнения (5.13) получается мнимым или комплексным. Для L или С могут получаться и по два различных действительных значения, удовлетворяющих уравнению (5.13). В таких случаях изменением L и С можно достичь двух различных резонансных режимов.

Решив уравнение (5.13) относительно w, найдем следующее значение для резонансной угловой частоты:

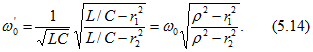
Резонанс возможен, если сопротивления и оба больше или оба меньше r. Если же это условие не выполнено, получается мнимая частота , т. е. не существует такой частоты, при которой имел бы место резонанс.

При резонансная частота , т. е. такая же, как и при резонансе в последовательном контуре.

При резонансная частота имеет любое значение, т. е. резонанс наблюдается на любой частоте. Действительно, при входное сопротивление контура

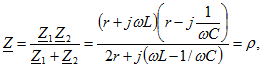
т. е. входное сопротивление контура активное и не зависит от частоты. Следовательно, ток совпадает по фазе с напряжением при любой частоте и его действующее значение равно .

Заметим, что в радиотехнике и электросвязи часто применяются контуры с малыми потерями, т. е. в них и малы по сравнению с r. В таких условиях резонансную частоту можно вычислять по формуле

Анализ, который здесь не приводится, показывает, что в общем случае сумма энергий электрического и магнитного полей при резонансе не остается постоянной. Эта сумма постоянна только в теоретическом случае, т. е. при .

Пример 5.2.

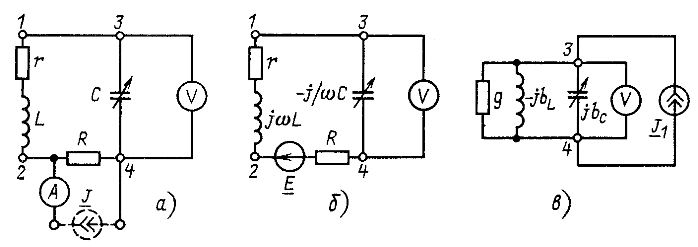
Угловая частота w и действующее значение I синусоидального тока, подводимого к цепи (рис. 5.7, а), поддерживаются неизменными. Емкость конденсатора без потерь изменяется до тех пор, пока при некотором значении С напряжение U, измеряемое вольтметром, не достигнет максимального значения Umax. По известным величинам w, I, С, Umax и R требуется определить параметры wL и r катушки, присоединенной к выводам 1 и 2.

Решение.

Проще всего задача решается путем преобразования схемы в эквивалентную, состоящую из переменного емкостного элемента с проводимостью , двух параллельно соединенных элементов - активной g, индуктивной проводимостей (рис. 5.7, в) и с источником тока подсоединенным к выводам 3 и 4.

В этой схеме при неизменном действующем токе и изменении емкости максимум напряжения, измеряемого вольтметром, будет наблюдаться при резонансе токов, так как входное сопротивление цепи при этом максимально.

В соответствии с намеченным путем решения приступаем к преобразованию схемы. Питание цепи (рис. 5.7, а) заданным током может рассматриваться как питание от источника тока (показан штриховой линией). Заменим источник тока источником ЭДС (рис. 5.7, б), а от источника ЭДС перейдем к новому источнику тока, подключенному к выводам 3 и 4. Ток этого источника