Частотные характеристики и резонансные кривые последовательного контура

Предположим, что к контуру (см. рис. 3.8) приложено синусоидальное напряжение , амплитуда которого неизменна, а частота может изменяться в пределах от 0 до .

Изменение частоты приводит к изменению параметров контура, изменяется его реактивное, а следовательно, и полное сопротивление, а также угол j (аргумент комплексного сопротивления). Зависимости от частоты параметров цепи назовем частотными характеристиками цепи, зависимости действующих или амплитудных значений тока и напряжения от частоты резонансными кривыми.

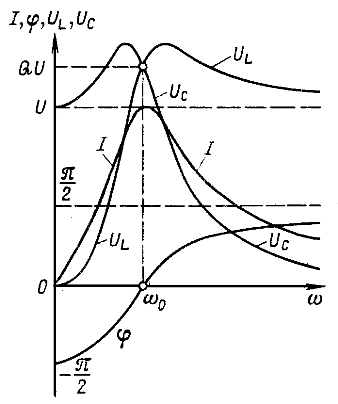
На рис. 5.1 построены частотные характеристики и . Изменение реактивного сопротивления приводит к изменению режима цепи. На рис. 5.2 приведен примерный вид резонансных кривых и кривой для цепи, добротность которой . При w = 0 напряжение, приложенное к цепи, во времени не изменяется, поэтому ток в цепи отсутствует. При изменении частоты от 0 до реактивное сопротивление имеет емкостный характер и изменяется от до 0 (см. рис. 5.1). Вследствие этого ток возрастает от 0 до максимального резонансного значения , а угол сдвига фаз между напряжением и током изменяется от -p/2 до 0. При изменении частоты от до результирующее реактивное сопротивление возрастает от 0 до и имеет индуктивный характер.

Вследствие этого ток уменьшается от наибольшего значения до 0, а угол j возрастает от 0 до p/2. Напряжение изменяется пропорционально току.

Дополнительно по теме

В выражении напряжения на индуктивности оба сомножителя зависят от частоты. При w = 0 сопротивление , ток I = 0, и, следовательно, . При изменении частоты от 0 до оба сомножителя увеличиваются и возрастает. При дальнейшем увеличении частоты () ток I уменьшается, но за счет роста wL напряжение продолжает возрастать. Анализ, который здесь не приводится, показывает, что для цепи с добротностью это возрастание продолжается непрерывно до значения U, а для цепи с добротностью напряжение при некоторой частоте достигает максимума , а затем уменьшается. При и , следовательно, .

Теперь рассмотрим зависимость напряжения на емкости от частоты. При w = 0 тока в цепи нет, поэтому . При возрастании w, начиная от нуля, непрерывно уменьшается. Анализ показывает, что для цепи с добротностью напряжение непрерывно уменьшается, а при напряжение сначала из-за возрастания тока I увеличивается, достигает при некотором значении частоты максимума , а затем уменьшается.

Уменьшение напряжения с ростом частоты начинается при частоте , меньшей , вследствие непрерывного уменьшения . При как I, так и равны нулю, поэтому . Заметим, что . При , как было отмечено, .

График зависимости тока от частоты показывает, что рассматриваемая цепь обладает "избирательными свойствами". Цепь обладает наименьшим сопротивлением для тока той частоты, которая наиболее близка к ее резонансной частоте.

Избирательными свойствами таких цепей широко пользуются в электросвязи и радиотехнике, при этом режим резонанса является нормальным режимом работы. Наоборот, в устройствах, где резонансный режим не предусмотрен, появление резонанса нежелательно, так как возникающие значительные напряжения на катушке и конденсаторе могут оказаться опасными для изоляции.

Рис. 5.1

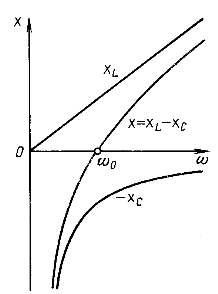
Рис. 5.2

Выясним влияние параметров цепи на форму резонансной кривой . Для удобства сравнения резонансных кривых друг с другом будем строить их в относительных единицах:

где - действующий ток при резонансе; - относительная частота.

Преобразуем выражение полного сопротивления цепи:

Разность характеризует расстройку контура относительно резонансной частоты. Произведение называется обобщенной расстройкой. С учетом этих обозначений сопротивление

Ток в цепи

Выражение (5.5) показывает, что влияние параметров цепи на вид резонансной кривой полностью учитывается добротностью Q.

На рис. 5.3,а представлен ряд резонансных кривых. Чем больше Q, тем острее резонансная кривая, тем лучше "избирательные свойства" цепи, что и послужило одной из причин назвать Q добротностью контура. Заметим, что наибольшие достигаемые на практике значения Q контуров, состоящих из катушек индуктивности и конденсаторов, лежат в пределах 200-500.

Для оценки избирательных свойств цепи вводят условное понятие ширины резонансной кривой или полосы пропускания контура , которую определяют как разность верхней и нижней частот, между которыми отношение превышает . На рис. 5.3, а проведена горизонтальная линия, соответствующая . Ее пересечение с резонансными кривыми определяет граничные частоты полосы пропускания соответствующих контуров. Из рисунка видно, что чем выше добротность, тем уже полоса пропускания контура.

Рис. 5.3

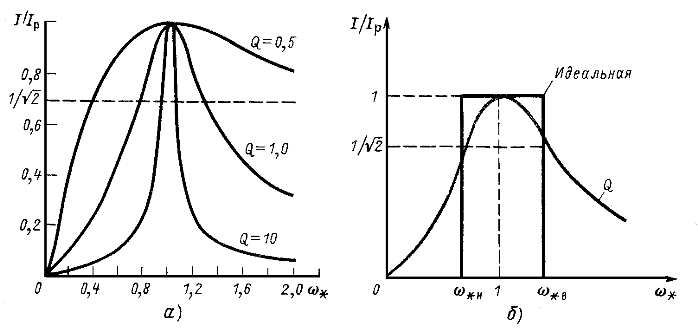
Высшая и низшая относительные частоты показаны на рис. 5.3,б для контура с известной добротностью Q. На этом же рисунке построена идеальная резонансная кривая, для которой вне полосы пропускания ток равен нулю, т. е. у которой идеальные избирательные свойства. На рис. 5.3, а также проведена горизонтальная линия, соответствующая . Ее пересечение с резонансными кривыми определяет полосы пропускания соответствующих контуров. Из рисунка видно, что чем выше добротность, тем уже полоса пропускания контура.

Если диапазон изменения частоты составляет несколько порядков, то часто выбирают для частоты логарифмический масштаб, т. е. или . Интервал частот , для которого , называют декадой (десятикратное изменение частоты). Число декад . Интервал частот, для которого , называют октавой (удвоение частоты), причем 1 декада октавы.