Работа и мощность тока. Закон Джоуля

Дополнительно по теме

1 Закон Кулона

2 Электрическое поле

3 Постоянный электрический ток

4 Работа и мощность тока. Закон Джоуля - Ленца

5 Электролиз. Законы Фарадея

6 Магнитное поле тока. Электромагнитная индукция

7 Переменный электрический ток

8 Электромагнитные колебания и волны

Работа и мощность тока. Закон Джоуля-Ленца

1 Какая энергия (в гектоватт-часах и джоулях) запасена в аккумуляторе с э.д.с. e = 2 В, имеющем емкость Q = 240 АЧч?

Решение:

Запасенная энергия

емкость аккумулятора Q = h; отсюда

2 Какой заряд пройдет по проводнику с сопротивлением R= 10 Ом за время t = 20с, если к его концам приложено напряжение V=12B? Какая при этом будет произведена работа?

Решение:

Заряд, прошедший по проводнику,

Произведенная при этом работа

3 Насколько изменится температура воды в сосуде, содержащем массу воды m = 0,2 кг, если через проводник, помещенный в него, прошел заряд q=100 Кл, а к концам проводника приложено напряжение V=20 В? Удельная теплоемкость воды с = 4,2 кДж/(кгЧК).

Решение:

Считая, что энергия, выделяющаяся в проводнике при прохождении тока, полностью идет на нагревание воды, имеем

где t1 и t2 - начальная и конечная температуры воды; отсюда изменение температуры воды

4 Можно ли вместо двух параллельно включенных электроплиток мощности N=500 Вт каждая включить в сеть электрокамин, который потребляет ток I=12,5 А при напряжении V=120B, если предохранитель рассчитан на ток, потребляемый плитками?

Решение:

При двух параллельно включенных в сеть плитках ток в общей цепи

Ток I= 12,5 А, потребляемый камином, больше, чем I1; поэтому нельзя ручаться за то, что предохранитель, выдерживающий ток при включении плиток, не перегорит при включении камина.

Работа и мощность тока. Закон Джоуля-Ленца

5 Найти площадь сечения проводов, отводящих ток от генератора мощности N=1 ГВт, если ток передается на трансформатор под напряжением V=15кВ. Плотность тока в проводе не должна превышать j= 10 А/мм2.

Решение:

Ток в проводах, идущих от генератора, I=N/V, а плотность тока j=I/S; отсюда площадь сечения проводов

6 Дуговая печь потребляет ток I=200 А от сети с напряжением V=120B через ограничивающее сопротивление R = 0,2 Ом. Найти мощность, потребляемую печью.

Решение:

N=I(V-IR)=16 кВт.

7 Нагревательная спираль электроаппарата для испарения воды имеет при температуре t=100°С сопротивление R= 10 Ом. Какой ток I надо пропускать через эту спираль, чтобы аппарат испарял массу воды m=100г за время t=1 мин? Удельная теплота парообразования воды l = 2,3 МДж/кг.

Решение:

Считая, что вся электрическая энергия затрачивается на испарение воды, получим

8 Электропечь должна давать количество теплоты Q = 0,1 МДж за время t = 10 мин. Какова должна быть длина нихромовой проволоки сечения S=0,5 мм2, если печь предназначается для сети с напряжением V=36 В? Удельное сопротивление нихрома r=1,2мкОмЧм.

Решение:

По закону Джоуля - Ленца

-сопротивление проволоки, l-ее длина; отсюда

9 Комната теряет в сутки количество теплоты Q = 87 МДж. Какой длины l надо взять нихромовую проволоку диаметра D = 1 мм для намотки электропечи, поддерживающей температуру комнаты неизменной? Печь включается в сеть с напряжением V=120В, удельное сопротивление нихрома r=1,2мкОмЧм.

Решение:

10 В сосуд, содержащий массу воды m = 480 г, помещен электронагреватель мощности N=40 Вт. Насколько изменилась температура воды в сосуде, если ток через нагреватель проходил в течение времени t = 21 мин? Удельная теплоемкость воды с=4,2 кДж/(кгЧК), теплоемкость сосуда вместе с нагревателем Сс=100Дж/К.

Решение:

Полученное количество теплоты идет на нагревание воды и сосуда с нагревателем, поэтому

где t1 и t2-начальная и конечная температуры воды. Изменение температуры воды

11 Найти мощность N электронагревателя кастрюли, если в ней за время t= 20 мин можно вскипятить объем воды V=2 л. К.п.д. электронагревателя h = 70%. Удельная теплоемкость воды с = 4,2 кДж/(кгЧК), начальная температура воды t1 = 20° С.

Решение:

Электрическая энергия, идущая на нагревание воды,

где

- масса воды, t2 = 100° С- конечная температура воды; отсюда

12 Сколько времени надо нагревать на электроплитке мощности N=600 Вт при к.п.д. h = 75% массу льда mл = 2кг, взятого при температуре t1 = —16° С, чтобы обратить его в воду, а воду нагреть до температуры t2 = 100°C? Удельная теплоемкость льда сл = 2,1 кДж/(кгЧК), удельная теплота плавления льда r=0,33 МДж/кг, удельная теплоемкость воды с = 4,2 кДж/(кгЧК).

Решение:

Время нагревания определяется из уравнения теплового баланса (tо=0°С):

13 Какова должна быть длина нихромовой проволоки диаметра D = 0,3 мм, чтобы при включении последовательно с 40-ваттной лампочкой, рассчитанной на 127 В, проволока давала нормальный накал при напряжении в сети V=220 В? Удельное сопротивление нихрома r= 1,2 мкОмЧм.

Решение:

14 Реостат с полным сопротивлением R подключен к сети с напряжением V (рис. 134). Во сколько раз изменится потребляемая от сети мощность, если движок реостата переместить на 1/4 длины от его конца?

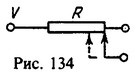
Решение:

Отношение выделяемых на реостате мощностей Nо/N=4/3.

15 Найти к.п.д. насосной установки, которая подает в единицу времени объем воды Vt = 75 л/с на высоту h = 4,7 м через трубу, имеющую сечение S=0,01 м2, если мотор потребляет мощность N=10 кВт.

Решение:

Для подачи воды на высоту А необходима мощность

К. п. д. установки

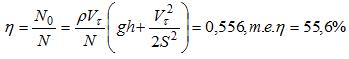
16 Моторы электропоезда при движении со скоростью u = 54км/ч потребляют мощность N=900 кВт. К.п.д. моторов и передающих механизмов h = 80%. Найти силу тяги F, развиваемую моторами.

Решение:

Мощность, необходимая для движения поезда, равна

отсюда

17 Железная и медная проволоки одинаковых длин и сечений соединены последовательно и включены в сеть. Найти отношение количеств теплоты, выделившихся в каждой проволоке. Удельные сопротивления железа и меди равны r1 =0,12 мкОмЧм и r2 = = 0,017 мкОмЧм. Решить эту же задачу для случая параллельного соединения проволок.

Решение:

Токи, идущие через обе проволоки, соединенные последовательно, одинаковы и равны I. При этом в проволоках за время t выделяются количества теплоты

-сопротивления железной и медной проволок, l и S-их длина и площадь сечения. Отношение количеств теплоты при последовательном соединении

При параллельном соединении токи в железной и медной проволоках

где V-напряжение в сети. В этом случае за время t в проволоках выделяются количества теплоты

Их отношение

18 Железная и медная проволоки одинаковых длин и сечений включены в сеть на равные промежутки времени сначала последовательно, затем параллельно. Найти отношение количеств теплоты, выделившихся в проволоках в обоих случаях, если по железной проволоке тек один и тот же ток. Удельные сопротивления железа и меди r1 =0,12 мкОмЧм и r2 = = 0,017 мкОмЧм.

Решение:

19 За время t1=40c в цепи из трех одинаковых проводников, соединенных параллельно и включенных в сеть, выделилось некоторое количество теплоты. За какое время t2 выделится такое же количество теплоты, если проводники соединить последовательно?

Решение:

20 Два одинаковых электронагревателя, потребляющих каждый мощность N = 200 Вт при напряжении V= 120 В, длинными и тонкими проводами подключены к источнику тока. Найти сопротивление проводов R, если при последовательном и при параллельном соединениях нагревателей они выделяют в единицу времени одно и то же количество теплоты.

Решение:

21 В электрочайнике с двумя нагревателями необходимо нагреть объем воды V=2 л от комнатной температуры (to = 20° С) до температуры кипения. Каждый нагреватель, включенный в сеть отдельно, выделяет мощность N1 = 250 Вт. Через какое время закипит вода, если ее подогревать одним нагревателем или двумя, включенными в ту же сеть последовательно или параллельно друг другу? К.п.д. нагревателя h = 80%. Удельная теплоемкость воды с = 4,2 кДж/(кгЧК).

Решение:

Для нагревания воды до температуры кипения t=100° С необходимо количество теплоты

масса воды в чайнике. При включении одного нагревателя его мощность N1=IV, где I-ток, текущий через него, и V-напряжение

сети. В этом случае на нагревание воды идет часть теплоты, выделяемой нагревателем,

отсюда время нагревания воды одним нагревателем

При параллельном включении двух нагревателей, как и при включении одного из них, на каждом нагревателе будет напряжение сети V. Следовательно, в каждом из них будет выделяться та же мощность N1 и общая мощность будет N2 = 2N1; отсюда время нагревания воды двумя нагревателями

При последовательном включении нагревателей общий ток через них будет равен 1/2. Поэтому общая мощность, выделяемая в них,

Следовательно, время нагревания воды в этом случае

22 Электрочайник имеет в нагревателе две секции. При включении первой секции вода в чайнике закипает за время t1 = 10 мин, а при включении второй секции — за время t2 = 40мин. Через какое время закипит вода, если включить обе секции параллельно или последовательно?

Решение:

При последовательном соединении секций

при параллельном соединении секций

23 Две лампы имеют одинаковые мощности. Одна из них рассчитана на напряжение V1 = 120 В, другая—на напряжение V2 = 220 В. Во сколько раз отличаются сопротивления ламп?

Решение:

Используя закон Джоуля-Ленца

находим

24 Какое сопротивление имеют 40- и 75-ваттные лампы, рассчитанные на включение в сеть с напряжением V=120 В? Какой ток течет через каждую лампу?

Решение:

Мощность лампы

где I-ток, текущий через лампу, R-ее сопротивление; отсюда для первой и второй ламп имеем

25 Какую мощность будет потреблять 25-ваттная лампочка, рассчитанная на напряжение V1 = 120 В, если ее включить в сеть с напряжением V2 = 220 В?

Решение:

26 100-ваттная лампа включена в сеть с напряжением V=120В. Сопротивление лампы в накаленном состоянии больше, чем в холодном (при температуре to = 0° С), в 10 раз. Найти температурный коэффициент сопротивления материала нити и сопротивление лампы в холодном состоянии, если во время горения лампы температура нити t = 2000° С.

Решение:

Когда лампа включена,

-сопротивление нити горящей лампы и Ro=R/10-сопротивление нити лампы при температуре t0; отсюда

27 Найти сопротивление 100-ваттной лампы при комнатной температуре to = 20° С, если при напряжении сети V=220 В температура нити t = 2800° С. Температурный коэффициент сопротивления материала нити .

Решение:

28 К источнику тока с э.д.с. e=140 В на расстоянии l=400 м от него подключена лампа, рассчитанная на напряжение V=120B и мощность N=100 Вт. Как изменится падение напряжения на лампе, если параллельно ей подключить вторую такую же лампу? Удельное сопротивление провода r = 0,028 мкОмЧм, его сечение S=1 мм2.

Решение:

Сопротивления лампы и проводов

Ток, текущий по линии, и падение напряжения на лампе равны

При подключении второй лампы сопротивление двух ламп равно R1/2. Поэтому ток, текущий по линии, и падение напряжения на лампах равны

Изменение напряжения на лампе

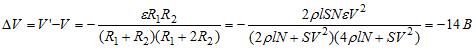
Знак минус показывает, что при включении второй лампы падение напряжения на первой уменьшается.

29 На какое расстояние l можно передавать электроэнергию от источника тока с э.д.с. e = 5 кВ так, чтобы на нагрузке с сопротивлением R=1,6кОм выделялась мощность N=10 кВт? Удельное сопротив¬ление провода r = 0,017 мкОмЧм, его сечение S=1 мм2.

Решение:

30 Под каким напряжением V нужно передавать электроэнергию на расстояние l=10 км, чтобы при плотности тока j = 0,5 А/мм2 в стальных проводах двухпроводной линии электропередачи потери в линии составляли 1% передаваемой мощности? Удельное сопротивление стали r = 0,12 мкОмЧм.

Решение:

31 Цепь состоит из двух параллельно включенных ламп мощности N=30 Вт каждая. Потери мощности в подводящих проводах составляют 10% полезной мощности. Найти напряжение на зажимах источника тока, если он обеспечивает в цепи ток I=2 A.

Решение:

Напряжение на зажимах источника тока

где V1 и V2 - падения напряжения на нагрузке и на проводах линии.

Мощность, выделяемая на нагрузке,

Потери мощности в линии

отсюда

32 От источника тока с напряжением V=750 В необходимо передать мощность N=5 кВт на некоторое расстояние. Какое наибольшее сопротивление R может иметь линия передачи, чтобы потери энергии в ней не превышали 10% передаваемой мощности?

Решение:

33 Какой наибольшей мощности электропечь можно установить в конце двухпроводной линии, имеющей сопротивление R=10 Ом, если источник тока развивает мощность N=6 кВт при напряжении V= 1 кВ?

Решение:

Ток в линии I=N/V. Потери мощности в линии

Мощность электропечи

34 Два параллельно соединенных резистора с сопротивлениями R1=6 0M И R2 = 12 0М подключены последовательно с резистором, имеющим сопротивление R= 15 Ом, к зажимам генератора с э.д.с. e = 200 В и внутренним сопротивлением r=1 Ом. Найти мощность, выделяющуюся на резисторе Rt.

Решение:

35 Элемент с э.д.с. e=12 В и внутренним сопротивлением r = 4 Ом замкнут на сопротивление R = 8 Ом. Какое количество теплоты будет выделяться во внешней цепи в единицу времени?

Решение:

Ток в цепи I=e/(R+r). Количество теплоты, выделяемое во внешней цепи в единицу времени,

36 Найти полную мощность элемента при сопротивлении внешней цепи R = 4 Ом, если внутреннее сопротивление элемента r = 2 Ом, а напряжение на его зажимах V=6 В.

Решение:

Полная мощность элемента

где I-ток в цепи. Так как

37 Батарея элементов, замкнутая на сопротивление R1 = 2 Ом, дает ток I1 = 1,6 А. Та же батарея, замкнутая на сопротивление R2 = 1 Ом, дает ток I2 = 2 А. Найти мощность, теряемую внутри батареи во втором случае.

Решение:

Внутри батареи теряется мощность

где r-внутреннее сопротивление батареи. Если e - э. д. с. батареи, то по закону Ома для полной цепи в первом и втором случаях

отсюда

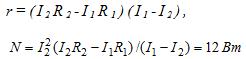
38 Найти э.д.с. e и внутреннее сопротивление r аккумулятора, если при токе I1 = 15 А он отдает во внешнюю цепь мощность N1=135 Вт, а при токе I2 = 6 А — мощность N2 = 64,8 Вт.

Решение:

39 К источнику тока с э.д.с. e = 8 В подключена нагрузка. Напряжение на зажимах источника V=6,4 В. Найти к.п.д. схемы.

Решение:

К. п. д.- это отношение полезной работы (мощности) ко всей затраченной работе (полной мощности). Полезной мощностью

в данном случае является мощность, выделяемая на нагрузке, N1=IV, где I-ток в цепи. Так как э. д. с. e по определению

представляет собой полную работу, совершаемую источником тока при перемещении по цепи единичного заряда, а в единицу времени через сечение проводника проходит заряд, численно равный I, то полная мощность источника тока равна

Таким образом, к.п.д. схемы

40 Найти к.п.д. схемы, изображенной на рис. 135. Сопротивления резисторов R1 = 2 Ом и R2 = 5 0M, внутреннее сопротивление источника тока r = 0,5 Ом.

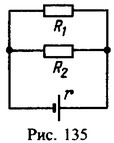
Решение:

41 Найти к.п.д. схемы, в которую включен элемент с э.д.с. e и внутренним сопротивлением r, если ток в цепи равен I. Выразить к.п.д.: через e, r и I через сопротивление внешней цепи R и внутреннее сопротивление элемента r; через э.д.с. элемента e и напряжение на его зажимах V.

Решение:

К. п. д. схемы

Так как

42 Найти ток 7 в цепи аккумулятора с э.д.с. e = 2,2 В, если сопротивление внешней цепи R = 0,5 Ом и к.п.д. схемы h = 65%.

Решение:

К.п.д. схемы

где V=IR - напряжение на зажимах источника; отсюда

43 Найти внутреннее сопротивление аккумулятора r, если при замене внешнего сопротивления R1 = 3 Ом на R2 = 10,5Ом к.п.д. схемы увеличился вдвое.

Решение:

44 Батарея из n = 6 последовательно включенных элементов с одинаковыми э.д.с. e=1,5 В питает током I=0,28 A две последовательно включенные лампы с сопротивлением R= 12,5 Ом каждая. Найти к.п.д. батареи и внутреннее сопротивление элемента.

Решение:

45 При включении электромотора в сеть с напряжением V=120 В он потребляет ток I=15 А. Найти мощность, потребляемую мотором, и его к.п.д., если сопротивление обмотки мотора R = 1 Ом.

Решение:

Полная мощность, потребляемая мотором,

На нагревание обмоток теряется мощность

Полезная мощность

К.п.д. мотора

Здесь не учтены потери мощности, возникающие вследствие нагревания сердечников якоря и статора вихревыми токами и вследствие трения в подшипниках.

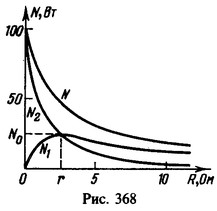
46 Найти зависимость: мощности N1 выделяемой во внешней цепи, мощности N2, выделяемой внутри источника тока, а также полной мощности N=N1+N2, развиваемой источником, от сопротивления внешней цепи R. Построить графики этих зависимостей. Э.д.с. источника e=15 В, его внутреннее сопротивление r = 2,5 Ом.

Решение:

Ток в цепи

Мощность, выделяемая во внешней цепи,

Мощность, выделяемая внутри источника тока,

Полная мощность

Из рис. 368 видно, что с увеличением R мощность N1, выделяемая во внешней цепи, сначала возрастает, а затем уменьшается. Чтобы найти сопротивление R, при котором выделяется максимальная полезная мощность, рассмотрим зависимость N1 от тока I:

Прибавив к этому выражению и отняв от него величину можно представить N1 в виде

отсюда следует, что максимальная полезная мощность выделяется при токе т.е. при R = r. В этом случае к.п.д.

Мощности N2 и N с увеличением R монотонно уменьшаются. При этом быстрее уменьшается мощность N2, выделяемая внутри источника. Поэтому с ростом R к. п. д. возрастает.

Из графика зависимости N1 от R видно также, что одна и та же полезная мощность может быть получена при двух значениях R, одно из которых больше, а другое меньше r.

47 Найти сопротивление R1 внешней цепи элемента, при котором мощность N, потребляемая во внешней цепи, такая же, как и при сопротивлении R2 = 10 Ом. Внутреннее сопротивление элемента r = 2,5 Ом.

Решение:

Если e -э. д. с. источника тока, то через сопротивление R1, течет ток

и во внешней цепи выделяется мощность

Через сопротивление R2 течет ток

и во внешней цепи выделяется мощность

отсюда для определения R1 получаем квадратное уравнение:

48 К аккумулятору с внутренним сопротивлением r=1 Ом подключен нагреватель с сопротивлением R = 8 Ом. Затем параллельно с первым подключили второй такой же нагреватель. Найти отношение количеств теплоты, выделяющихся в единицу времени во внешней цепи.

Решение:

49 К источнику тока с внутренним сопротивлением r=1 Ом подключаются два резистора с сопротивлением R = 0,5 Ом каждый. Один раз резисторы подключаются последовательно, другой раз — параллельно. Найти отношение мощностей, выделяющихся во внешней цепи в обоих случаях.

Решение:

50 Батарея состоит из параллельно соединенных элементов с э.д.с. e = 5,5 В и внутренним сопротивлением r = 5 Ом. При токе во внешней цепи I=2 А полезная мощность N=1 Вт. Сколько элементов имеет батарея?

Решение:

51 Нагреватель, имеющий сопротивление R = 25 Ом, питается от двух одинаковых аккумуляторов с внутренним сопротивлением r=10Ом. Параллельно или последовательно следует соединить аккумуляторы, чтобы получить в нагревателе большую мощность?

Решение:

большая мощность - при параллельном соединении.

52 Электровоз массы m = 300 т движется вниз по горе со скоростью u = 36 км/ч. Уклон горы a = 0,01, сила сопротивления движению электровоза составляет 3% от действующей на него силы тяжести. Какой ток протекает через мотор электровоза, если напряжение в сети V=ЗкВ и к.п.д. электровоза h = 80%?

Решение:

Проекция силы тяжести в направлении движения

меньше силы сопротивления f=0,03mg. Поэтому мотор совершает работу против равнодействующей этих сил. За время х эта работа

где I-ток, текущий через мотор; отсюда

53 Из одного пункта в другой передается электроэнергия, питающая установку мощности N=62 кВт. Сопротивление проводов линии R = 5 Ом. Найти падение напряжения в линии, потери мощностей в ней и к.п.д. передачи, если передача осуществляется при напряжениях V1 = 6200 В и V2 = 620 В.

Решение:

При напряжении на зажимах источника тока V и силе тока в линии I мощность источника

отсюда ток в линии

Два значения тока соответствуют двум возможным сопротивлениям нагрузки, при которых на нагрузке выделяется одна и та же мощность. Знак минус перед корнем соответствует меньшему току, а следовательно, и меньшим потерям мощности в линии. Падение напряжения и потери мощности в линии

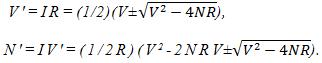
К. п. д. передачи (отношение мощности, потребляемой установкой, к мощности, отдаваемой источником в линию)

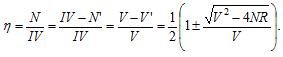
При V= V1 = 6200 В падение напряжения и потери мощности в линии V'= 50 В (или 6150 В) и N' = 508 Вт (или 7,6 МВт); к. п. д. передачи h= 99,8% (или 0,8%). Цифры в скобках соответствуют большему значению тока. При V=V2= 620 В под корнем получается отрицательное число. Это значит, что при сопротивлении линии R=5 0м в этом случае нельзя получить требуемую мощность ни при каком значении сопротивления нагрузки.

54 Какое сопротивление R должен иметь резистор из нихромовой проволоки, включенный последовательно с лампой, чтобы лампа горела нормальным накалом при напряжении V=220 В, если лампа рассчитана на напряжение Vo = 120 В при мощности N = 60 Вт? Найти длину l проволоки, если ее удельное сопротивление r = 1,0 мкОмЧм, а ее сечение S=0,5 мм.

Решение:

55 Найти мощность N, выделяющуюся во внешней цепи, состоящей из двух резисторов с сопротивлением R каждый, если на резисторах выделяется одна и та же мощность как при последовательном, так и при параллельном соединении. Э.д.с. источника тока e=12 В, его внутреннее сопротивление r = 2 Ом.

Решение:

56 Какую мощность N потребляет схема, изображенная на рис. 136? Э.д.с. элемента e=12 В, его внутреннее сопротивление r = 0,4 Ом. Сопротивления резисторов R1=2 0м, R2=4 0м, R3 = ЗОм, R4 = 6 Ом и R5 = 10Ом.

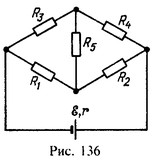
Решение:

Из условия

следует, что ток через резистор R5 не идет. Поэтому полное сопротивление R цепи складывается из сопротивлений двух параллельных цепочек R1, R2 и R3, R4 и внутреннего сопротивления элемента r.

Схема потребляет мощность

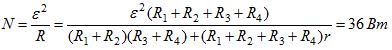
57 Три одинаковых элемента с э.д.с. e и резисторы с сопротивлением R каждый включены в цепь, изображенную на рис. 137. Найти мощность, выделяющуюся на всех сопротивлениях схемы.

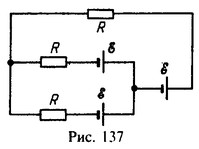
Решение:

58 Для составления елочной гирлянды имеется n1 = 10 лампочек мощности N=2 Вт при номинальном напряжении V1 =4 В и некоторое число лампочек, имеющих ту же мощность при номинальном напряжении V2 = 8 В. Какое минимальное число n2 8-вольтовых лампочек нужно взять, чтобы, добавив их к десяти 4-вольтовым, составить гирлянду для включения в сеть с напряжением Vo = 120 В?

Решение:

Через лампочку должен течь ток I=N/V, где V-номинальное напряжение, т. е. 4-вольтовые лампочки рассчитаны на ток

0,5 А, а 8-вольтовые - на ток 0,25 А. Следовательно, необходимо смешанное включение: последовательно с десятью 4-вольтовыми

лампочками нужно включить параллельно друг другу две одинаковые группы 8-вольтовых лампочек. Падение напряжения на дополнительных группах 8-вольтовых лампочек будет

а число лампочек в обеих группах должно быть

59 Источник тока замыкают первый раз на сопротивление R1 = 9 0м, второй раз — на сопротивление R2 = 4 0м. Оба раза за одно и то же время на сопротивлениях выделяется одно и то же количество теплоты. Найти внутреннее сопротивление r источника.

Решение:

60 При одном и том же напряжении одна лампа потребляет мощность, в два раза большую, чем другая. Найти мощности N1 и N2, потребляемые каждой лампой при их последовательном включении в цепь, если вместе они в этом случае потребляют мощность N.

Решение:

61 От источника тока необходимо передать потребителю мощность No = 4кBт. Сопротивление подводящих проводов R = 0,4 Ом. Какое напряжение должно быть на зажимах источника, чтобы потери мощности в проводах составляли 4% потребляемой мощности?

Решение:

Потери мощности в подводящих проводах

Ток в них

Падение напряжения на нагрузке

Падение напряжения на подводящих проводах

Напряжение на зажимах источника

62 Конденсатор емкости С1, имеющий заряд q1, соединяют через резистор с конденсатором емкости С2, имеющим заряд q2. Какое количество теплоты Q выделяется на резисторе? Соединяются противоположно заряженные обкладки.

Решение:

Общий заряд на соединенных обкладках

Емкость образовавшегося конденсатора

Энергия, запасенная в конденсаторах до и после соединения,

На резисторе выделилось количество теплоты

63 Найти энергию W батареи конденсаторов, изображенной на рис. 138, при разомкнутом и замкнутом ключе К. Емкости конденсаторов С1 = С, С2 = 2С, С3 = С/2, С4 = С. Э.д.с. источника тока равна e.

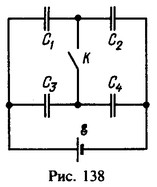
Решение:

При разомкнутом ключе К конденсаторы С1 и С2 имеют заряды q; напряжения на них

причем

Аналогично находим заряды и напряжения на конденсаторах

Так как V1 = V3, потенциалы обкладок конденсаторов, присоединенных к ключу, одинаковы. При замыкании ключа ничего не изменяется. Полная энергия батареи конденсаторов равна сумме энергий, запасенных в каждом из них:

Дополнительно по теме

1 Закон Кулона

2 Электрическое поле

3 Постоянный электрический ток

4 Работа и мощность тока. Закон Джоуля - Ленца

5 Электролиз. Законы Фарадея

6 Магнитное поле тока. Электромагнитная индукция

7 Переменный электрический ток

8 Электромагнитные колебания и волны