Закон Ома для полной цепи

Дополнительно по теме

1 Закон Кулона

2 Электрическое поле

3 Постоянный электрический ток

4 Работа и мощность тока. Закон Джоуля - Ленца

5 Электролиз. Законы Фарадея

6 Магнитное поле тока. Электромагнитная индукция

7 Переменный электрический ток

8 Электромагнитные колебания и волны

Закон Ома для полной (замкнутой) цепи

1 В цепи источника тока с э. д. с. e = 30 В идет ток I=2 А. Напряжение на зажимах источника V=18 В. Найти внешнее сопротивление цепи R и внутреннее сопротивление источника r.

Решение:

Напряжение на внешнем сопротивлении цепи V=I/R. Ток в цепи I=e/(R+r); отсюда R=V/I=6 0м, r=(e-V)/I=4 Ом.

2 В цепи, состоящей из реостата и источника тока с э. д. с. e = 6 В и внутренним сопротивлением r = 2 Ом, идет ток I1 = 0,5 А. Какой ток I2 пойдет при уменьшении сопротивления реостата в три раза?

Решение:

По закону Ома для цепи I1=e/(R+r) и I2=e/(R/3+r), где R—сопротивление реостата. Исключив из этих уравнений R, найдем

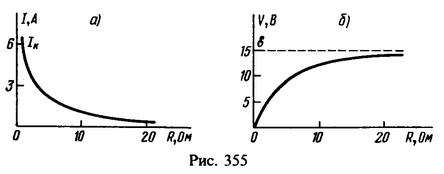
3 Источник тока с э. д. с. e и внутренним сопротивлением r замкнут на сопротивление R. Как меняется ток в цепи и напряжение на зажимах источника в зависимости от R?

Построить графики этих зависимостей при e =15 В и r = 2,5 Ом.

Решение:

Ток в цепи I=e/(R+r). Напряжение на зажимах источника тока V=I/R=eR/(R+r). При R=0 через источник течет ток короткого замыкания Ik = 6 А. С увеличением R ток стремится к нулю (по гиперболическому закону) (рис. 355, а), а напряжение стремится к э. д. с. e = 15 В (рис. 355, б).

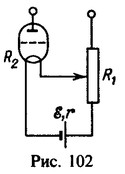
4 Нить накала радиолампы включена последовательно с реостатом в цепь источника тока с э. д. с. e = 2,5 В и внутренним сопротивлением r = 0,1 Ом (рис. 102). Необходимый ток накала достигается, когда сопротивление реостата R1 = 8,4 Ом. Найти ток в цепи накала I, если сопротивление нити накала R2 = 30 Ом.

Решение:

Ток цепи накала

Закон Ома для полной (замкнутой) цепи

5 Для питания нити накала радиолампы необходимы напряжение V=4B и ток I=1А. Найти дополнительное сопротивление R1 при котором в цепи накала достигается необходимый ток (рис. 102). Э. д. с. источника тока e=12 В, его внутреннее сопротивление r = 0,6 Ом.

Решение:

Сопротивление нити накала R2 = V/I. Ток накала при наличии дополнительного сопротивления R1 в цепи

отсюда

6 Лампа подключена медными проводами к источнику тока с э. д. с. e= 2 В и внутренним сопротивлением r= 0,04 Ом. Длина проводов l=4м, их диаметр D = 0,8 мм, удельное сопротивление меди r = 0,017 мкОмЧм. Напряжение на зажимах источника V=1,98B. Найти сопротивление лампы R.

Решение:

7 Вольтметр, подключенный к источнику тока с э. д. с. e=120В и внутренним сопротивлением r = 50Ом, показывает напряжение V=118В. Найти сопротивление вольтметра R.

Решение:

8 При подключении внешней цепи напряжение на зажимах источника тока с э. д. с. e = 30 В оказывается равным V=18 B. Внешнее сопротивление цепи R = 6 Ом. Найти внутреннее сопротивление источника r.

Решение:

Напряжение на зажимах источника тока равно падению напряжения на внешнем сопротивлении цепи: V=IR, где I=e/(R+r) отсюда r=R(e-V)/V=4 Ом.

9 Источник тока с э. д. с. e=1,25 В и внутренним сопротивлением r = 0,4 Ом питает лампу, рассчитанную на напряжение V1 = 1 В. Сопротивление лампы R1 = 10 Ом. Найти сопротивление подводящих проводов R2 и напряжение на них V2.

Решение:

Ток в цепи

Падение напряжения на лампе и подводящих проводах V1 = IR1 и V2 = IR2. Из этих уравнений находим

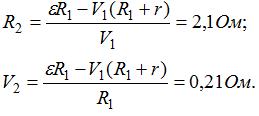
10 Источник тока питает n=100 ламп, рассчитанных на напряжение К, = 220 В и соединенных параллельно. Сопротивление каждой лампы R1 = 1,2кОм, сопротивление подводящих проводов R2 = 4 Ом, внутреннее сопротивление источника r = 0,8 Ом.

Найти напряжение на зажимах источника и его э. д. с.

Решение:

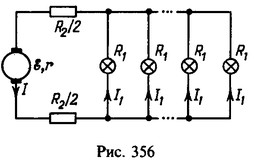Через каждую лампу течет ток I1 = V1/R1 (рис. 356). Ток в общей цепи I=nI1=nV1/R1. Напряжение в подводящих проводах

Напряжение на зажимах источника тока и его э. д. с.

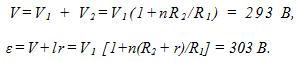
11 Какова должна быть э. д. с. e источника тока в схеме, изображенной на рис. 103, чтобы напряженность электрического поля в плоском конденсаторе была E=2,25 кВ/м? Внутреннее сопротивление источника r = 0,5 Ом, сопротивление резистора R = 4,5 Ом, расстояние между пластинами конденсатора d=0,2 см.

Решение:

12 Источник тока с э. д. с. e = 15 В и внутренним сопротивлением r = 5 Ом замкнут на резистор с сопротивлением R=10Ом. К зажимам источника подключен конденсатор емкости С=1 мкФ. Найти заряд на конденсаторе.

Решение:

13 Электрическая цепь состоит из источника тока и двух последовательно соединенных резисторов с одинаковыми сопротивлениями R. К концам одного из резисторов присоединяют по очереди два вольтметра: один имеет сопротивление R,

а другой — сопротивление 10R. Во сколько раз будут отличаться показания вольтметров?

Решение:

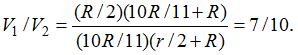
14 К источнику тока с э. д. с. e = 8,8 В присоединены последовательно резистор с неизвестным сопротивлением Rx и резистор с сопротивлением R2 = 1 кОм. Вольтметр с сопротивлением R = 5 кОм, подключенный к концам резистора показывает напряжение V=4 В. Какое падение напряжения V` будет на резисторе R1 если отключить вольтметр?

Решение:

15 Какой ток I покажет амперметр в схеме, изображенной на рис. 104? Сопротивления резисторов R1 = 1,25 Ом, R2=1 Ом, R3=3 Ом, R4=7 Ом, э.д.с. источника e= 2,8 В.

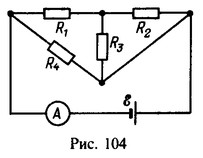
Решение:

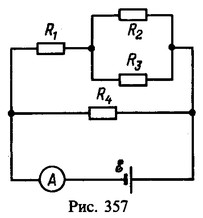Изобразим схему иначе (рис. 357). Заменим сопротивления резисторов R1, R2 и R3 сопротивлением

Тогда полное сопротивление цепи

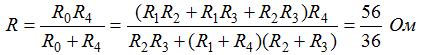
и амперметр покажет ток I= e/R = 1,8 А.

16 Найти ток I, идущий через источник тока в схеме, изображенной на рис. 105. Сопротивления всех резисторов одинаковы и равны R = 34 Ом, э. д. с. источника e = 73 В.

Решение:

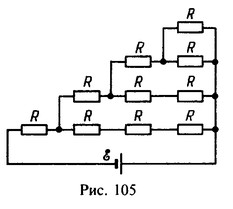
17 Найти ток I, идущий через резистор с сопротивлением R2 в схеме, параметры которой даны на рис. 106.

Решение:

Падения напряжения на резисторах R1 и R2, а также на резисторах 2R1 и 2R2 пропорциональны их сопротивлениям. Поэтому падение напряжения на резисторе R равно нулю и ток через него не проходит. Через резистор R2 течет ток

18 Один полюс источника тока с э. д. с. e= 1400 В и внутренним сопротивлением r = 2,2 Ом подключен к центральной алюминиевой жиле кабеля (диаметр жилы D1 = 8мм), другой — к его свинцовой оболочке (наружный диаметр D2 =18 мм, внутренний — d2 = 16 мм). На каком расстоянии l от источника кабель порвался и произошло замыкание жилы с оболочкой, если начальный ток короткого замыкания I=120 А? Удельные сопротивления алюминия и свинца r1 =0,03 мкЧОм м и r2 = 0,2 мкОЧмм.

Решение:

Полное сопротивление цепи R= R1 + R2 + r, где сопротивления жилы и оболочки до места замыкания

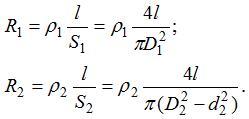
Ток в цепи I= e/R; отсюда

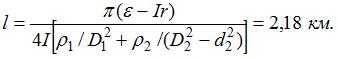
19 Найти ток I, текущий через резистор с сопротивлением К1 в схеме, параметры которой даны на рис. 107, в первый момент после замыкания ключа, если до этого напряжение на конденсаторе было постоянным.

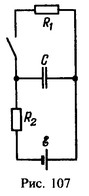
Решение:

Напряжение на конденсаторе V=e. Это же напряжение будет в первый момент после замыкания ключа на резисторе R1. Поэтому текущий через него в этот момент ток I=e/R1.

20 Найти напряжения V1 и V2 на конденсаторах с емкостями С1 и С2 в схеме, параметры которой даны на рис. 108.

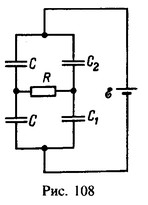
Решение:

После включения источника тока с э. д. с. e конденсаторы зарядятся, и, когда ток прекратится, все их обкладки, соединенные с резистором R, будут иметь одинаковый потенциал. Конденсаторы с емкостями С+С1 и С+С2 включены последовательно с источником тока. Общее напряжение на них V1+V2 =e, а заряд на них

отсюда

21 Найти заряды q1, q2 и q3 на каждом из конденсаторов в схеме, параметры которой даны на рис. 109.

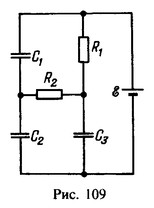
Решение:

Обкладки конденсатора C1замкнуты через резисторы R1 и R2. Поэтому заряд на этом конденсаторе q1=0 (после прекращения зарядки конденсаторов С2 и С3). Так как после зарядки конденсаторов токи в схеме не протекают, то напряжения на конденсаторах С2 и С3 равны e. Следовательно,

22 В цепь, питаемую источником тока с внутренним сопротивлением r = 3 Ом, входят два резистора с одинаковыми сопротивлениями R1 = R2 = 28 Ом, вклю-ченные параллельно, и резистор с сопротивлением R3 = 40 Ом (рис.110). Параллельно резистору R3 подключен конденсатор емкости С=5 мкФ, заряд которого q=4,2 Кл. Найти э. д. с. e источника.

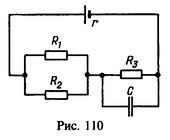
Решение:

Падение напряжения на резисторе R3 будет V=q/C=IR3; отсюда ток, текущий через этот резистор, I=q/CR3. Полное сопротивление цепи и э. д. с. источника тока

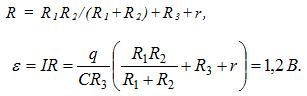
23 Два резистора с одинаковыми сопротивлениями R1 =25 Ом и резистор с сопротивлением R2 = 50 Ом подключены к источнику тока по схеме, изображенной на рис. 111. К участку ab подключен конденсатор емкости С = 5 мкФ. Найти э. д. с. e источника тока, если заряд на конденсаторе q = 0,11 мКл.

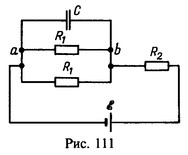
Решение:

24 Найти заряд на конденсаторе емкости С в схеме, параметры которой даны на рис. 112.

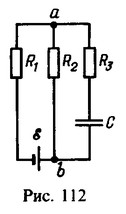
Решение:

Сопротивление конденсатора постоянному току бесконечно велико. Поэтому после зарядки конденсатора по резистору R3 ток протекать не будет. Не будет и падения напряжения на этом езисторе. Следовательно, точка а и верхняя обкладка конденсатора будут иметь одинаковый потенциал. Потенциал же точки b будет равен потенциалу нижней обкладки конденсатора. Таким образом, напряжение на конденсаторе будет равно падению напряжения на резисторе R2. Ток в цепи

отсюда заряд на конденсаторе

25 Найти напряжение на конденсаторе емкости в схеме, параметры которой даны на рис. 113.

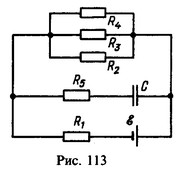
Решение:

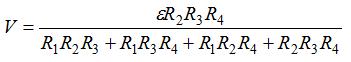
26 Источник тока с внутренним сопротивлением r=10м замкнут на резистор с сопротивлением R. Вольтметр, подключенный к зажимам источника, показывает напряжение V1=20B. Когда параллельно резистору с сопротивлением R присоединен резистор с таким же сопротивлением R, показание вольтметра уменьшается до V2 = 15B. Найти сопротивление резистора R, если сопротивление вольтметра велико по сравнению с R.

Решение:

Напряжения на зажимах источника тока в первом и во втором случаях V1=I1R и V2=I2R/2. Токи в общей цепи в этих случаях

отсюда

27 К источнику тока с э. д. с. e = 200 В и внутренним сопротивлением r = 0,5 Ом подключены последовательно два резистора с сопротивлениями R1 = 100Ом и R2 = 500 Ом. К концам резистора R2 подключен вольтметр. Найти сопротивление R вольтметра, если он показывает напряжение V=160 В.

Решение:

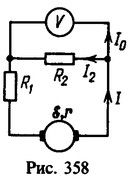Падение напряжения на резисторе R2 (и на вольтметре) V=IRо (рис. 358), где Rо = R2R/(R2 + R)-сопротивление параллельно включенных вольтметра и резистора R2. Ток в общей цепи равен

Решая совместно эти уравнения, получим

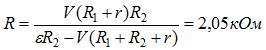
Тот же результат можно получить, решая систему уравнений

28 Проволока из нихрома изогнута в виде кольца радиуса а=1 м (рис.114). В центре кольца помещен гальванический элемент с э. д. с. e = 2 В и внутренним сопротивлением r=1,5 0м. Элемент соединен с точками с и d кольца по диаметру с помощью такой же нихромовой проволоки. Найти разность потенциалов между точками cad. Удельное сопротивление нихрома r=1,1мкОмЧм, площадь сечения проволоки S= 1 мм2.

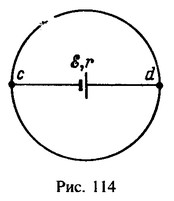
Решение:

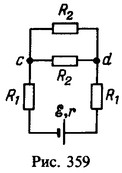В эквивалентной схеме резисторы R1 соответствуют проволокам, соединяющим элемент с кольцом, а резисторы R2-двум половинам кольца (рис. 359). Полное внешнее сопротивление цепи

Ток в общей цепи

Разность потенциалов между точками с и d

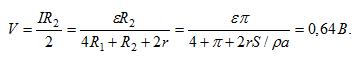
29 К источнику тока с внутренним сопротивлением r = 1 Ом подключены два параллельно соединенных резистора с сопротивлениями R1 = 10 Ом и R2 = 2 Ом. Найти отношение токов, протекающих через резистор R1 до и после обрыва в цепи

резистора R2.

Решение:

30 Два резистора с сопротивлениями R1 = R2 = 1 Ом и реостат, имеющий полное сопротивление R3 = 2 Ом, присоединены к источнику тока с внутренним сопротивлением r = 0,5 Ом (рис. 115). К разветвленному участку цепи подключен вольтметр. Когда движок реостата находится на его середине (точка а), вольтметр показывает напряжение Vа=13 В. Каково будет показание вольтметра, если движок передвинуть в крайнее правое положение на реостате? Сопротивление вольтметра велико по сравнению с R1 и R2.

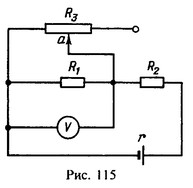
Решение:

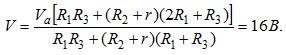
31 Шесть проводников с одинаковыми сопротивлениями R0 = 2 Ом соединены попарно параллельно. Все три пары соединены последовательно и подключены к источнику тока с внутренним сопротивлением r=1 Ом. При этом по каждому проводнику течет ток I0 = 2,5А. Какой ток будет течь по каждому проводнику, если один из них удалить?

Решение:

Сопротивление каждой пары проводников равно Ro/2. Полное внешнее сопротивление цепи до удаления одного из проводников R1=3Rо/2. По закону Ома для полной цепи

отсюда э. д. с. источника тока

После удаления одного из проводников полное внешнее сопротивление цепи

Ток в общей цепи

Через проводник, оставшийся без пары, будет идти ток

а через остальные проводники будут идти токи I2/2 = 2 А.

32 Источник тока с э. д. с. e = 100 В и внутренним сопротивлением r = 0,2 Ом и три резистора с сопротивлениями R1= 3 Ом, R2 = 2 Ом и R3 = 18,8 Ом включены по схеме, изображенной на рис. 116. Найти токи, текущие через резисторы R1 и R2.

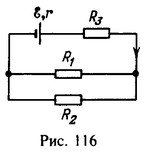
Решение:

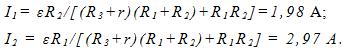
33 К источнику тока с э. д. с. e=120 В и внутренним сопротивлением r=10Ом подключены два параллельных провода с сопротивлениями R1 =20 Ом. Свободные концы проводов и их середины соединены друг с другом через две лампы с сопротивлениями R2 = 200 Ом. Найти ток, текущий через источник тока.

Решение:

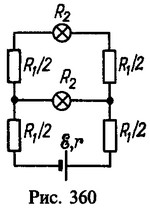Верхняя лампа и провода, идущие к ней, начиная от места присоединения нижней лампы (рис. 360), образуют последовательную цепочку с сопротивлением R3=R1+R2. Эта цепочка соединена параллельно с нижней лампой и вместе с ней образует сопротивление

Полное внешнее сопротивление цепи

Через источник тока течет ток

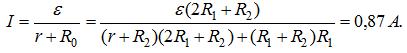
34 При замыкании источника тока на резистор с сопротивлением R1=5 Ом в цепи идет ток I1 = 5 А, а при замыкании на резистор с сопротивлением R2 = 2 0м идет ток I2 = 8 А. Найти внутреннее сопротивление r и э. д. с. источника тока e.

Решение:

Если e и r - э. д. с. и внутреннее сопротивление источника тока, то

Из этих уравнений имеем

35 При замыкании источника тока на резистор с сопротивлением R1 = 14 Ом напряжение на зажимах источника V1 = 28 В, а при замыкании на резистор с сопротивлением R2 = 29 Ом напряжение на зажимах V2 = 29 В. Найти внутреннее сопротивление r источника.

Решение:

36 Амперметр с сопротивлением R1 = 2 Ом, подключенный к источнику тока, показывает ток I1 = 5 А. Вольтметр с сопротивлением R2 = 150 Ом, подключенный к такому же источнику тока, показывает напряжение V=12B. Найти ток короткого замыкания Iк источника.

Решение:

При подключении к источнику тока амперметра через него течет I1=e/(R1+r), где e - э. д. с. батареи, а r-ее внутреннее сопротивление; при подключении к источнику тока вольтметра через него течет ток I2= e/(R2+r), и вольтметр показывает напряжение

отсюда

Ток короткого замыкания (при равном нулю внешнем сопротивлении)

37 Два параллельно соединенных резистора с сопротивлениями R1=40 Ом и R2 = 10 Ом подключены к источнику тока с э. д. с. e=10 В. Ток в цепи I=1 А. Найти внутреннее сопротивление источника и ток короткого замыкания.

Решение:

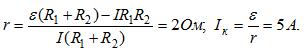
38 Аккумулятор с э. д. с. e = 25 В и внутренним сопротивлением r = 1 Ом заряжается от сети с напряжением V=40 В через сопротивление R = 5 Ом. Найти напряжение Va на зажимах аккумулятора.

Решение:

При зарядке аккумулятор включается навстречу источнику тока. Во время зарядки ток внутри аккумулятора течет от положительного полюса к отрицательному. Напряжение сети V=e+I(R+r), где I-ток зарядки; отсюда I=(V-e)/(R+r). Напряжение на зажимах аккумулятора

Дополнительно по теме

1 Закон Кулона

2 Электрическое поле

3 Постоянный электрический ток

4 Работа и мощность тока. Закон Джоуля - Ленца

5 Электролиз. Законы Фарадея

6 Магнитное поле тока. Электромагнитная индукция

7 Переменный электрический ток

8 Электромагнитные колебания и волны