Переходные процессы при «некорректных» коммутациях

До сих пор рассматривались такие цепи и режимы их работы, для которых удовлетворялись законы коммутации

где t = (0 -) - момент времени непосредственно перед коммутацией, a t = = (0 +) - момент времени сразу после коммутации.

Рассмотрим теперь такие цепи и их режимы, для которых законы коммутации (14.111) не соблюдаются ("некорректные" коммутации). Пусть в цепи, питаемой от источника постоянного напряжения U (рис. 14.47), мгновенно отключается ветвь с резистором . Токи во всех ветвях непосредственно перед коммутацией легко определяются. После коммутации ток i в контуре, составленном из первой и второй ветвей, удовлетворяет дифференциальному уравнению

решение которого

где .

Для определения постоянной А нельзя воспользоваться первой из формул (14.111), гак как до отключения ветви с сопротивлением токи

были различны, а после ее отключения они, очевидно, одинаковы, и, в частности, в первый момент после коммутации . Значит, токи в момент разрыва третьей ветви ключом (мгновенного) должны измениться скачком, что приведет к возникновению бесконечно больших напряжений на индуктивных элементах. Но так как токи во всех ветвях схемы на рис. 14.47 конечны, то для промежутка коммутации (от t = 0- до t = 0 + ) алгебраическая сумма бесконечно больших напряжений на индуктивных элементах и напряжений на резистивных элементах должна уравновеситься приложенным напряжением U:

Интегрируя это равенство за промежуток коммутации, т.е. от t = 0- до t = 0 + , и учитывая, что ввиду конечности правой части при t = 0 и стремления промежутка интегрирования к нулю интеграл от правой части равен нулю, получаем

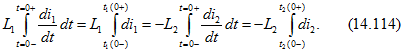
Перепишем (14.114) так:

или

Из (14.115) следует, что потокосцепление контура y, составленного из первой и второй катушек (иначе говоря, сумма потокосцеплений с обеими катушками), до и после отключения ветви осталось неизменным:

Отсюда находим

далее из (14.113) находим постоянную

Рис. 14.47

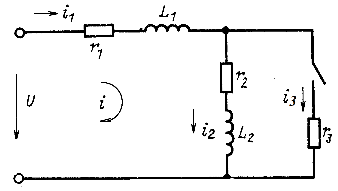
Рис. 14.48

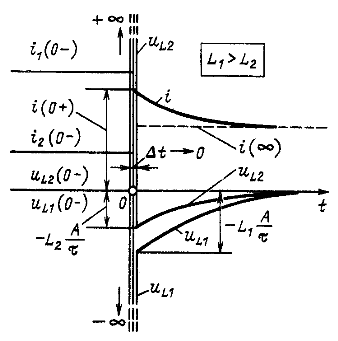
Следует иметь в виду, что бесконечно большие напряжения на индуктивных элементах противоположных знаков (рис. 14.48, построен в предположении, что А > 0) появились вследствие предположения о том, что коммутация произошла за бесконечно малый промежуток времени: . Эти импульсы напряжения имеют бесконечно малую длительность. Но интегралы от этих импульсов (14.114) имеют конечные значения и равны приращениям потокосцеплений каждой из катушек. На том же рис. 14.48 показано, что токи в катушках при t = 0 изменяются скачком и ток i в катушках после отключения ветви с сопротивлением изменяется в соответствии с постоянной времени t и стремится к значению

Подчеркнем, что разность энергий, запасенных в магнитных полях обеих катушек до коммутации,

и после коммутации

т. е.

положительна и расходуется на выделение тепла в сопротивлении искры или дуги, которая может появиться между контактами выключателя, и на возможное излучение энергии. При решении задачи была принята идеализация процесса выключения, т. е. мгновенная коммутация. На самом деле она происходит хотя и весьма быстро, но за конечное время . При этом в сопротивлении возникающей между контактами выключателя электрической искре и расходуется часть энергии . Кроме того, катушки индуктивности обладают распределенной емкостью между витками и между расходящимися контактами выключателя существует емкость, что приводит к образованию сложного колебательного контура, который может излучать энергию (на высокой частоте), на что расходуется другая часть энергии . Если учесть все эти процессы, то никакие бесконечно большие напряжения на индуктивных элементах не возникнут и токи в них не будут изменяться скачком, т. е. будут справедливы законы коммутации (14.111), сформулированные в разделе.

И в других цепях с катушками индуктивности при "некорректных" коммутациях, приводящих к скачкам токов в индуктивных элементах, постоянные интегрирования следует определять с применением обобщенного первого закона коммутации - неизменности в момент коммутации потокосцеплений контуров, или более подробно: потокосцепление любого замкнутого контура в первый момент после коммутации (t = 0 + ) равно алгебраической сумме потокосцеплений всех входящих в него индуктивных элементов, которые последние имели непосредственно перед коммутацией (t = 0 - ); некоторые из этих индуктивных элементов перед коммутацией могли и не составлять замкнутого контура, а образовали его лишь после коммутации.

Рис. 14.49

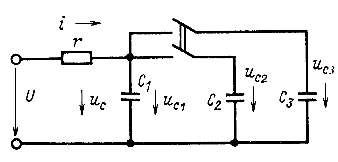
Рассмотрим теперь процессы, возникающие, например, при одновременном включении двух заряженных до разных напряжений конденсаторов к заряженному до напряжения U конденсатору (рис. 14.49). Полагаем, что сопротивления проводов, соединяющих конденсаторы , пренебрежимо малы. Поэтому постоянные времени, обусловленные ими, также ничтожны. При этих условиях напряжения на всех трех конденсаторах в момент замыкания ключа могут изменяться скачком и через них могут проходить бесконечно большие токи. Все три конденсатора до включения рубильника были заряжены до различных напряжений и имели заряды

Токи конденсаторов будут существовать только в течение бесконечно малого промежутка времени перезарядки от t = 0 - до t = 0 +. Так как напряжение источника U и сопротивление последовательного участка цепи r конечны, го суммарный ток r должен оставаться конечным и импульсы токов в трех параллельно соединенных конденсаторах должны взаимно уравновешиваться, т. е.

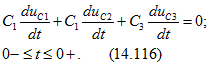
Интегрируя это равенство по времени t = 0- до t = 0 +

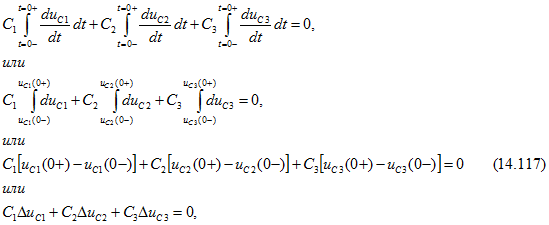
приходим к равенству

Отсюда следует, что изменение зарядов на всех параллельно включенных конденсаторах за время коммутации равно нулю, т. е. сумма зарядов конденсаторов перед коммутацией (t = 0 -) равна сумме их зарядов непосредственно после коммутации (t = 0 + ) -закон сохранения заряда или второй обобщенный закон коммутации. Этот же результат получается, если учесть, что после коммутации (t = 0 + ) напряжения на всех параллельно включенных конденсаторах равны:

На основании (14.117) и (14.118) получаем

откуда определяется .

Все три конденсатора заменяются одним с емкостью , и напряжение на нем после коммутации определяется дифференциальным уравнением

решение которого известно:

где t=rС.

На основании сказанного выше , поэтому

и ток

Легко показать, что энергия, запасенная в конденсаторах до коммутации,

больше энергии электрического поля эквивалентного конденсатора С после коммутации

а избыток ее

перейдет в тепло в сопротивлениях контактов ключа, сопротивлениях проводов и в энергию излучения сложного колебательного контура, который получится, если учесть, что соединительные провода всегда имеют индуктивность, хотя и очень малую.

Подчеркнем, что при наличии сопротивлений во всех трех ветвях с конденсаторами напряжения на них в момент коммутации скачком не изменяются, токи в них остаются конечными, т. е. выполняется второй закон коммутации, сформулированный в разделе.

Дополнительно по теме