Периодическая (колебательная) разрядка конденсатора
Разрядка будет периодической или колебательной, если сопротивление контура меньше критического: ![]() , т. е. корни характеристического уравнения ( 14.34) комплексные и сопряженные.
, т. е. корни характеристического уравнения ( 14.34) комплексные и сопряженные.
Обозначим в ( 14.35)
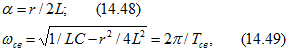
так что
![]()
где ![]() - угловая частота и
- угловая частота и ![]() - период собственных или свободных колебаний контура.
- период собственных или свободных колебаний контура.
Для корней ![]() получим
получим
![]()
Решение дифференциального уравнения ( 14.32) при комплексных корнях его характеристического уравнения удобно записать в виде
![]()
(но можно и в виде суммы двух экспонент с комплексными показателями).
Ток
![]()
Так как переходные напряжение и ток попрежнему равны их свободным значениям и начальные условия такие же, как и в двух предыдущих случаях, то по формулам (14.52) и (14.53) получим
![]()
Из последних соотношений находим
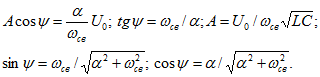
Подставив значения ![]() в (14.52) и (14.53) и обозначив для краткости
в (14.52) и (14.53) и обозначив для краткости
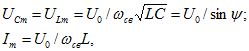
получим окончательные выражения:
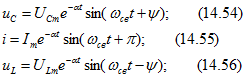
Кривые изменения ![]() и i даны на рис. 14.19. Ток и напряжения представляются затухающими синусоидальными функциями с угловой частотой собственных колебаний контура
и i даны на рис. 14.19. Ток и напряжения представляются затухающими синусоидальными функциями с угловой частотой собственных колебаний контура ![]() и коэффициентом затухания a, причем как
и коэффициентом затухания a, причем как ![]() , так и a определяются только параметрами контура r, L и С. Начальная фаза y зависит также только от параметров контура, в то время как
, так и a определяются только параметрами контура r, L и С. Начальная фаза y зависит также только от параметров контура, в то время как ![]() зависят и от параметров контура, и от начального напряжения на конденсаторе.
зависят и от параметров контура, и от начального напряжения на конденсаторе.
Быстроту затухания рассматриваемых колебаний характеризуют отношением напряжений в моменты времени t и ![]() :
:
![]()
Это отношение, называемое декрементом колебания, - постоянная величина, не зависящая от времени t, а зависящая лишь от параметров rLC-контура.
Часто быстроту затухания колебаний характеризуют натуральным логарифмом этого отношения
![]()
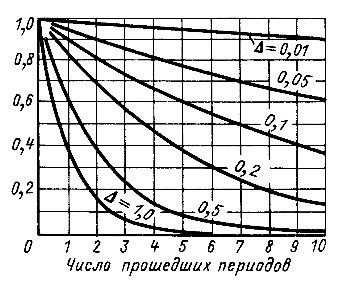
который называется логарифмическим декрементом колебания. Если кривая затухает медленно, то отношение ее значений, отстоящих на время ![]() друг от друга, близко к единице, логарифмический декремент близок к нулю. На рис. 14.20 представлены кривые изменения отношения амплитуд колебаний в конце 1, 2, 3-го и т. д. периодов к начальной амплитуде, построенные для разных значений логарифмического декремента
друг от друга, близко к единице, логарифмический декремент близок к нулю. На рис. 14.20 представлены кривые изменения отношения амплитуд колебаний в конце 1, 2, 3-го и т. д. периодов к начальной амплитуде, построенные для разных значений логарифмического декремента ![]() .
.
Рис. 14.19
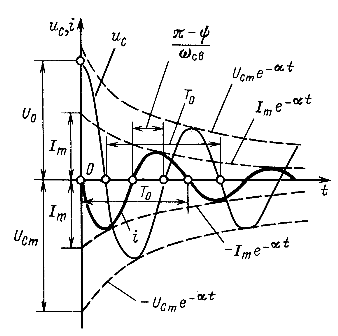
Рис. 14.20
Сопротивление r оказывает существенное влияние на скорость затухания колебательной разрядки конденсатора. Кроме того, как показывает равенство (14.49), по мере увеличения сопротивления r уменьшается частота собственных колебаний ![]() и увеличивается их период
и увеличивается их период ![]() . Когда r достигнет значения
. Когда r достигнет значения ![]() , частота собственных колебаний будет равна нулю, период - бесконечности, что соответствует апериодической разрядке.
, частота собственных колебаний будет равна нулю, период - бесконечности, что соответствует апериодической разрядке.
При колебательной разрядке конденсатора через идеальную катушку (r = 0) получим
![]()
т. е. затухание процесса равно нулю, а частота собственных колебаний имеет наибольшее возможное значение и равна резонансной частоте последовательного контура.
Из равенств (14.54) - (14.56) следует, что ![]() будут изменяться гармонически с угловой частотой
будут изменяться гармонически с угловой частотой ![]() :
:
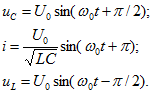
Ток i отстает по фазе на p/2 от напряжения на индуктивном и опережает на p/2 напряжение на емкостном элементах. Поскольку сопротивление отсутствует, первоначальный запас энергии остается неизменным и энергия попеременно переходит из электрического поля в магнитное, и наоборот.
Дополнительно по теме
- Переходные процессы в электрических цепях
- Возникновение переходных процессов и законы коммутации
- Переходный, установившийся и свободный процессы
- Короткое замыкание rL-цепи
- Включение rL-цепи на синусоидальное напряжение
- Короткое замыкание rС-цепи
- Включение rC-цепи на постоянное напряжение
- Включение rC-цепи на синусоидальное напряжение
- Переходные процессы в rС-цепи
- Апериодическая разрядка конденсатора
- Предельный случай апериодической разрядки конденсатора
- Включение rLC-цепи на постоянное напряжение
- Общий случай расчета переходных процессов классическим методом
- Пример классического метода
- Переходные процессы в цепях с взаимной индуктивностью
- Включение пассивного двухполюсника к источнику непрерывно меняющегося напряжения
- Включение пассивного двухполюсника к источнику напряжения произвольной формы
- Переходная и импульсная переходная характеристики
- Запись интеграла Дюамеля при помощи импульсной переходной характеристики
- Метод переменных состояния
- Численные методы решения уравнений состояния
- Дискретные модели электрической цепи
- Переходные процессы при некорректных коммутациях
- Определение переходного процесса при воздействии периодических импульсов напряжения

